
【题目】已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,且函数
,且函数![]() 的部分图象如图所示:
的部分图象如图所示:
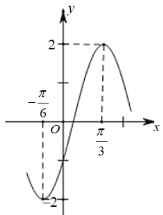
(1)求![]() 的大小;
的大小;
(2)若![]() ,点
,点![]() 为线段
为线段![]() 上的点,且
上的点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中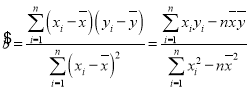 ,
,![]() ,
, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加竞答游戏,一轮三个题目,每人回答一题为体现公平,制定如下规则:
①第一轮回答顺序为甲、乙、丙;第二轮回答顺序为乙、丙、甲;第三轮回答顺序为丙,甲、乙;第四轮回答顺序为甲、乙、丙;…,后面按此规律依次向下进行;
②当一人回答不正确时,竞答结束,最后一个回答正确的人胜出.
已知,每次甲回答正确的概率为![]() ,乙回答正确的概率为
,乙回答正确的概率为![]() ,丙回答正确的概率为
,丙回答正确的概率为![]() ,三个人回答每个问题相互独立.
,三个人回答每个问题相互独立.
(1)求一轮中三人全回答正确的概率;
(2)分别求甲在第一轮、第二轮、第三轮胜出的概率;
(3)记![]() 为甲在第
为甲在第![]() 轮胜出的概率,
轮胜出的概率,![]() 为乙在第
为乙在第![]() 轮胜出的概率,求
轮胜出的概率,求![]() 与
与![]() ,并比较
,并比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某市![]() 年全社会固定资产投资以及增长率如图所示,则下列说法错误的是( )
年全社会固定资产投资以及增长率如图所示,则下列说法错误的是( )
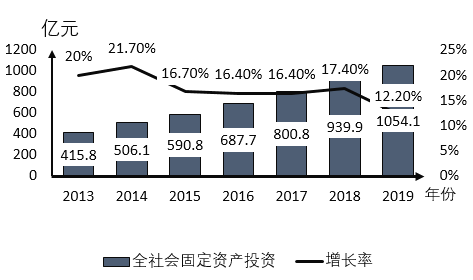
A.从2013年到2019年全社会固定资产的投资处于不断增长的状态
B.从2013年到2019年全社会固定资产投资的平均值为![]() 亿元
亿元
C.该市全社会固定资产投资增长率最高的年份为2014年
D.2016年到2017年全社会固定资产的增长率为0
查看答案和解析>>
科目:高中数学 来源: 题型:
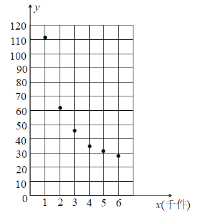
【题目】2020年初全球爆发了新冠肺炎疫情,为了防控疫情,某医疗科研团队攻坚克难研发出一种新型防疫产品,该产品的成本由原料成本及非原料成本组成,每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,根据已经生产的统计数据,绘制了如下的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用函数![]() 对两个变量的关系进行拟合.参考数据(其中
对两个变量的关系进行拟合.参考数据(其中![]() ):
):
|
|
|
|
|
|
|
0.41 | 0.1681 | 1.492 | 306 | 20858.44 | 173.8 | 50.39 |
(1)求y关于x的回归方程,并求y关于u的相关系数(精确到0.01).
(2)该产品采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为80元,则签订9千件订单的概率为0.7,签订10千件订单的概率为0.3;若单价定为70元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为30元,根据(1)的结果,要想获得更高利润,产品单价应选择80元还是70元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,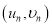 ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: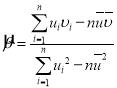 ,
,![]() ,相关系数
,相关系数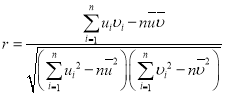 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是:
①在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差;
②回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
③在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量
中,当解释变量每增加1个单位时,预报变量![]() 平均增加0.1个单位
平均增加0.1个单位
④若![]() ,
,![]() ,则
,则![]() ;
;
⑤已知正方体![]() ,
,![]() 为底面
为底面![]() 内一动点,
内一动点,![]() 到平面
到平面![]() 的距离与到直线
的距离与到直线![]() 的距离相等,则
的距离相等,则![]() 点的轨迹是抛物线的一部分.
点的轨迹是抛物线的一部分.
正确的序号是:______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com