Question

【题目】已知函数f（x）=Asin（ωx+ ）（A＞0，ω＞0）的图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0 ， 2）和（x0+ ，﹣2）．
（1）求函数f（x）的解析式；
（2）求sin（x0+ ）的值．

Answer 1

【答案】
（1）解：∵图象在y轴右侧的第一个最高点和第一个最低点的坐标分别为（x0，2）和（x0+ ，﹣2）．

∴A=2， =x0+ ﹣x0= ，

即函数的周期T=π，即T= ，解得ω=2，

即f（x）=2sin（2x+ ）

（2）解：∵函数的最高点的坐标为（x0，2），

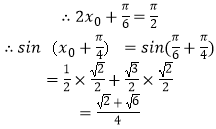
∴2x0+ = ，

即x0= ，

则sin（x0+ ）=sin（ + ）=sin cos +cos sin

= （sin +cos ）= （ ）=

【解析】（1）根据条件求出振幅以及函数的周期，即可求函数f（x）的解析式；（2）根据函数的最值，求出x0的大小，结合两角和差的正弦公式进行求解即可．
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：．