
分析 (Ⅰ)得到-2,m是方程x2-2x+2a=0的根,组成方程组,解出即可;
(Ⅱ)通过讨论c的范围结合二次函数的性质求出c的范围即可.
解答 解:(Ⅰ)∵f(x)≤0的解集为{x|-2≤x≤m},
∴-2,m是方程x2-2x+2a=0的根,
∴$\left\{\begin{array}{l}{4+4+2a=0}\\{{m}^{2}-2m+2a=0}\end{array}\right.$,
解得:a=-4,m=4;
(Ⅱ)由(Ⅰ)得:a=-4,
(c+a)x2+2(c+a)x-1<0,
即(c-4)x2+2(c-4)x-1<0,
c-4=0,即c=4时,-1<0,成立,
c-4≠0时,
若关于x的不等式(c+a)x2+2(c+a)x-1<0恒成立,
则$\left\{\begin{array}{l}{c-4<0}\\{△={4(c-4)}^{2}+4(c-4)<0}\end{array}\right.$,
解得:$\frac{13}{4}$<c<4,
综上,$\frac{13}{4}$<c≤4.
点评 本题考查了二次函数的性质,考查函数恒成立问题,是中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
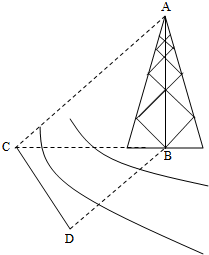 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=75°,∠BDC=45°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 30$\sqrt{2}$米 | B. | 30$\sqrt{6}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 10$\sqrt{6}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z | B. | x=kπ+$\frac{π}{8}$,k∈Z | C. | x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z | D. | x=kπ+$\frac{3π}{8}$,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{256}$ | B. | $\frac{1}{512}$ | C. | $\frac{1}{1024}$ | D. | $\frac{1}{2048}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com