
正三棱柱ABC-A1B1C1的棱长都为2,E,F,G为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为( ).

A. B.
B. C.
C.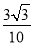 D.
D.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-3练习卷(解析版) 题型:解答题
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-3练习卷(解析版) 题型:选择题
若双曲线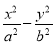 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=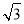 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
A.(1,2) B.(1,2] C.(1,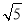 ) D.(1,
) D.(1,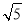 ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-1练习卷(解析版) 题型:填空题
直线y=2x+3被圆x2+y2-6x-8y=0所截得的弦长等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:解答题
已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G,H分别是CE,CF的中点.
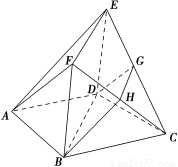
(1)求证:平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°,求直线CF与平面BDGH所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.

(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=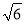 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:选择题
如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).
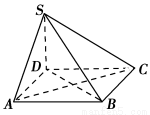
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-2练习卷(解析版) 题型:解答题
在等差数列{an}中,a3+a4+a5=84,a9=73.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中落入区间(9m,92m)内的项的个数记为bm,求数列{bm}的前m项和Sm.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:解答题
已知函数f(x)= x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com