
【题目】已知函数f(x)=ax+blnx(a,b∈R)在点(1,f(1))处的切线方程为y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)当x>1时,f(x)![]() 0恒成立,求实数k的取值范围;
0恒成立,求实数k的取值范围;
(3)设g(x)=ex![]() x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
【答案】(1)a![]() ,b=1.(2)k∈
,b=1.(2)k∈![]() .(3)见解析
.(3)见解析
【解析】
(1)求导数,利用切线方程可得![]() ,从而可求得
,从而可求得![]() ;
;
(2)x>1时,f(x)![]() 0恒成立,转化为
0恒成立,转化为![]() 恒成立,求
恒成立,求![]() 的最小值即可;
的最小值即可;
(3)g(x)﹣f(x)﹣2=ex![]() x﹣(
x﹣(![]() x+lnx)﹣2=ex﹣lnx﹣2>0在x∈(0,+∞)上恒成立.
x+lnx)﹣2=ex﹣lnx﹣2>0在x∈(0,+∞)上恒成立.
ex﹣x﹣1>lnx﹣x+1在x∈(0,+∞)上恒成立.这样只要求得![]() 的最小值,
的最小值,![]() 的最大值,即可证明.
的最大值,即可证明.
(1)f′(x)=a![]() .
.
函数f(x)=ax+blnx(a,b∈R)在点(1,f(1))处的切线方程为y![]() x﹣1.
x﹣1.
∴![]() =a+b
=a+b![]() ,f(1)=a
,f(1)=a![]() 1,
1,
解得a![]() ,b=1.
,b=1.
(2)f(x)![]() x+lnx,
x+lnx,
当x>1时,f(x)![]() 0恒成立,
0恒成立,
等价于:k![]() ,x∈(1,+∞).
,x∈(1,+∞).
令u(x)![]() x2﹣xlnx,x∈(1,+∞).
x2﹣xlnx,x∈(1,+∞).
则u′(x)=x﹣lnx﹣1,
令v(x)=x﹣lnx﹣1,x∈(1,+∞).
∴v′(x)=1![]() 0,
0,
∴u′(x)=x﹣lnx﹣1>u′(1)=0,
∴u(x)在x∈(1,+∞)上单调递增.
∴k≤u(1)![]() .
.
∴k∈![]() .
.
(3)证明:设g(x)=ex![]() x,
x,
g(x)﹣f(x)﹣2=ex![]() x﹣(
x﹣(![]() x+lnx)﹣2=ex﹣lnx﹣2>0在x∈(0,+∞)上恒成立.
x+lnx)﹣2=ex﹣lnx﹣2>0在x∈(0,+∞)上恒成立.
ex﹣x﹣1>lnx﹣x+1在x∈(0,+∞)上恒成立.
令F(x)=ex﹣x﹣1,x∈(0,+∞).G(x)=lnx﹣x+1,x∈(0,+∞).
F′(x)=ex﹣1,x∈(0,+∞).
则F′(x)>F′(0)=0,
∴F(x)>F(0)=0.
G′(x)![]() ,
,
可得x=1时,函数G(x)取得极大值即最大值,
∴G(x)≤G(1)=0.
∴g(x)﹣f(x)﹣2>0在x∈(0,+∞)上恒成立.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]() 有以下三个判断
有以下三个判断
①函数恒有两个零点且两个零点之积为-1;
②函数恒有两个极值点且两个极值点之积为-1;
③若![]() 是函数的一个极值点,则函数极小值为-1.
是函数的一个极值点,则函数极小值为-1.
其中正确判断的个数有( )
A.0个B.1个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,
, ![]() ,则称
,则称![]() 为“D-数列”.
为“D-数列”.
(1)举出一个前六项均不为零的“D-数列”(只要求依次写出该数列的前六项);
(2)若“D-数列”![]() 中,
中,![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,分别判断当
,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值(若不存在不需要交代理由);
的极限是否存在?如果存在,求出其极限值(若不存在不需要交代理由);
(3)证明:任何“D-数列”中总含有无穷多个为零的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1,2. 第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2; 那么第10次“H扩展”后得到的数列的所有项的和为( )
A.88572B.88575C.29523D.29526
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公比大于
是公比大于![]() 的等比数列,
的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.数列
成等差数列.数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 满足
满足![]() ,且
,且![]() ,
,
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令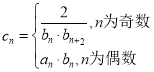 ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() ;
;
(3)将数列![]() ,
,![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为 _____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种掷硬币走跳棋的游戏:在棋盘上标有第1站、第2站、第3站、…、第100站,共100站,设棋子跳到第![]() 站的概率为
站的概率为![]() ,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
,一枚棋子开始在第1站,棋手每掷一次硬币,棋子向前跳动一次.若硬币的正面向上,棋子向前跳一站;若硬币的反面向上,棋子向前跳两站,直到棋子跳到第99站(失败)或者第100站(获胜)时,游戏结束.
(1)求![]()
![]()
![]() ;
;
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com