
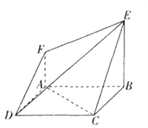
【题目】如图,在空间几何体ABCDFE中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() ,
,![]() .
.
(1)求证:AC//平面DEF;
(2)已知![]() ,若在平面
,若在平面![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置.
的位置.
【答案】(1)证明见解析;(2)![]() 是线段
是线段![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.
【解析】试题分析:
(1)连BD交AC于O,取DE中点K,连结OK、KF,由题意结合三角形中位线的性质可得四边形AOKF为平行四边形,则![]() ,由线面平行的判断定理可得AC//平面DEF
,由线面平行的判断定理可得AC//平面DEF
(2)由题意,以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系.由题意可得
轴建立空间直角坐标系.由题意可得![]() ,
,![]() ,设
,设![]() ,计算可得
,计算可得![]() ,由
,由 可得方程组,求解方程组有
可得方程组,求解方程组有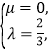 即
即![]() .
.![]() 是线段
是线段![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.
试题解析:
(1)连BD交AC于O,取DE中点K,连结OK、KF
∵AC、BD是正方形![]() 的对角线
的对角线
∴O为BD中点,∴![]() ,∴四边形AOKF为平行四边形,∴
,∴四边形AOKF为平行四边形,∴![]()
又∵![]() 平面DEF,
平面DEF,![]() 平面DEF
平面DEF
∴AC//平面DEF
(2)在△DAF中,![]() ,
,![]() ,
,![]() ,所以
,所以![]()
又因为![]() ,
,![]() ,
,![]() 平面ABCD
平面ABCD
∴![]() 平面
平面![]() .
.
以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
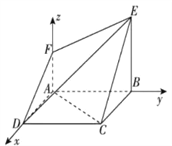
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设![]() ,因为
,因为![]() ,
,![]() ,
,
又![]() ,
,![]()
![]()
所以![]() ,
,
∵ ∴
∴![]()
解得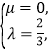 即
即![]() .所以
.所以![]() 是线段
是线段![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的右顶点和上顶点,且
的右顶点和上顶点,且![]() .
.
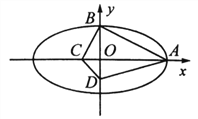
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
,![]() 分别是
分别是![]() 轴负半轴,
轴负半轴,![]() 轴负半轴上的点,且四边形
轴负半轴上的点,且四边形![]() 的面积为2,设直线
的面积为2,设直线![]() 和
和![]() 的交点为
的交点为![]() ,求点
,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为_____,动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线x2=8
,它的一个顶点恰好是抛物线x2=8![]() y的焦点.
y的焦点.
(1)求椭圆C的标准方程;
(2)直线x=﹣2与椭圆交于P,Q两点,A,B是椭圆上位于直线x=﹣2两侧的动点,若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣alnx+(a+1)x﹣![]() (a>0).
(a>0).
(1)讨论函数f(x)的单调性;
(2)若f(x)≥﹣![]() +ax+b恒成立,求a
+ax+b恒成立,求a![]() 时,实数b的最大值.
时,实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同。若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度![]() 与时间t满足关系式:
与时间t满足关系式:![]() ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度![]() 与时间t满足关系式:
与时间t满足关系式: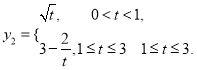 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰。
(1)若a=1,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值?
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 为圆
为圆![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() .
.
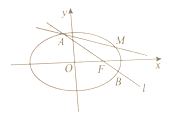
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)如图,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点.
轴的对称点.
(1)求证:![]() ;
;
(2)试问过![]() ,
,![]() 的直线是否过定点?若是,请求出该定点;若不是,请说明理由.
的直线是否过定点?若是,请求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )

A. 平面ABD⊥平面ABC B. 平面ADC⊥平面BDC
C. 平面ABC⊥平面BDC D. 平面ADC⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com