
【题目】下列命题:
①动点M到二定点A、B的距离之比为常数![]() 则动点M的轨迹是圆
则动点M的轨迹是圆
②椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]()
③双曲线![]() 的焦点到渐近线的距离是
的焦点到渐近线的距离是![]()
④已知抛物线![]() 上两点
上两点![]() (
(![]() 是坐标原点),则
是坐标原点),则![]()
以上命题正确的是( )
A.②③④B.①④
C.①③D.①②③
【答案】D
【解析】
对于①,通过建立坐标系,求出动点的轨迹方程判断出正确;利用椭圆中三个参数的关系判断出②对;对于③,据双曲线的方程求出焦点坐标和渐近线方程,利用点到直线的距离公式判断出正确;对于④,利用向量垂直的充要条件判断出其错
对于①,以AB所在的直线为x轴,AB的中垂线为y轴建立坐标系,设M(x,y),A(-a,0),B(a,0),则有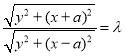 化简得(1-λ2)x2+(1-λ2)y2+(2a+2aλ2)x+a2-a2λ2=0,所以动点M的轨迹是圆,①正确;
化简得(1-λ2)x2+(1-λ2)y2+(2a+2aλ2)x+a2-a2λ2=0,所以动点M的轨迹是圆,①正确;
对于②,![]() ,所以
,所以![]() ,所以a2=2c2,所以椭圆中有b2=a2-c2=c2,所以b=c,所以②正确;
,所以a2=2c2,所以椭圆中有b2=a2-c2=c2,所以b=c,所以②正确;
对于③,双曲线![]() 的焦点坐标为(±c,0),渐近线的方程为:
的焦点坐标为(±c,0),渐近线的方程为:![]() ,根据点到直线的距离公式得到距离=
,根据点到直线的距离公式得到距离=![]() .所以③正确;
.所以③正确;
对于④,因为OA⊥OB,所以x1x2+y1y2=0,又因为y2=2px,所以y12=2px1,y22=2px2,所以y1y2=-4p2.④不正确
故选:D.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知函数![]() 的图象在
的图象在![]() 上连续不断,定义:
上连续不断,定义:
![]()
![]() ,
,
![]()
![]() .
.
其中,![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函数
表示函数![]() 在
在![]() 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“
上的“![]() 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若![]() ,
,![]() ,试写出
,试写出![]() ,
,![]() 的表达式;
的表达式;
(Ⅱ)已知函数![]() ,
,![]() ,试判断
,试判断![]() 是否为
是否为![]() 上的“
上的“![]() 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的![]() ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知![]() ,函数
,函数![]() 是
是![]() 上的2阶收缩函数,求
上的2阶收缩函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
高一(7)班 |
| 6 |
| 4 | 5 | 6 | 5 | 2 | 3 |
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求![]() 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取![]() 位同学,设随机变量
位同学,设随机变量![]() 为投票给地理学科的人数,求
为投票给地理学科的人数,求![]() 的分布列和期望;
的分布列和期望;
(Ⅲ)当![]() 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
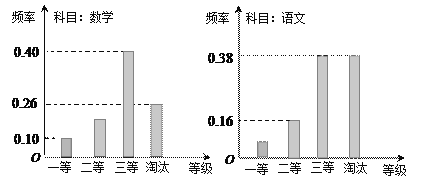

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这![]() 科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各
科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各![]() 人进行模拟选科.经统计,选择全文的人数比不选全文的人数少
人进行模拟选科.经统计,选择全文的人数比不选全文的人数少![]() 人.
人.

(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
附: ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知10件不同产品中有3件是次品,现对它们一一取出(不放回)进行检测,直至取出所有次品为止.
(1)若恰在第5次取到第一件次品,第10次才取到最后一件次品,则这样的不同测试方法数有多少?
(2)若恰在第6次取到最后一件次品,则这样的不同测试方法数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对现有设备进行了改造,为了了解设备改造后的效果,现从设备改造前后生产的大量产品中各抽取了100件产品作为样本,检测其质量指标值,若质量指标值在![]() 内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内,则该产品视为合格品,否则视为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

(1)完成![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关:
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价180元;质量指标值落在
内的定为一等品,每件售价180元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价150元;其他的合格品定为三等品,每件售价120元.根据频数分布表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com