练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．如图，三棱锥P-ABC的体积为12，D为PB中点，且EF$\stackrel{∥}{=}$MN$\stackrel{∥}{=}$$\frac{1}{2}$AC，则三棱柱BEF-DMN的体积为$\frac{9}{2}$

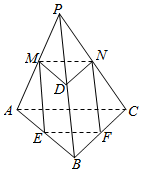
    分析 由条件可知E，F，M，N为棱锥P-ABC的对应边的中点，于是棱柱的底面积为棱锥底面积的$\frac{1}{4}$，高为棱锥的$\frac{1}{2}$．

    解答 解：∵EF$\stackrel{∥}{=}$MN$\stackrel{∥}{=}$$\frac{1}{2}$AC，∴MN，EF为△PAC，△ABC的中位线，
    ∴S△BEF=$\frac{1}{4}{S}_{△ABC}$，D到平面ABC的距离h为P到底面距离的$\frac{1}{2}$．
    ∵VP-ABC=$\frac{1}{3}{S}_{△ABC}•2h=12$，∴S△ABC•h=18．
    ∴VBEF-DMN=S△BEF•h=$\frac{1}{4}{S}_{△ABC}•h$=$\frac{9}{2}$．
    故答案为：$\frac{9}{2}$．

    点评 本题考查了棱锥，棱柱的体积计算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1、F2，若椭圆上存在一点P使得∠F1PF2=90°，且|PF1|是|PF2|和|F1F2|的等差中项，则椭圆的离心率e为（　　）
    A．$\frac{5}{7}$B．$\frac{2}{3}$C．$\frac{4}{5}$D．$\frac{\sqrt{3}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．随机变量X的分布列如下，则m=（　　）
    X1234
    P$\frac{1}{4}$m$\frac{1}{3}$$\frac{1}{6}$
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{1}{6}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图，三棱柱ABC-A1B1C1中，D，M分别为CC1和A1B的中点，A1D⊥CC1，侧面ABB1A1为菱形且∠BAA1=60°，AA1=A1D=2，BC=1，
    （Ⅰ）证明：直线MD∥平面ABC；
    （Ⅱ）求二面角B-AC-A1的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线方程是y=$\frac{4}{3}$x，则该双曲线的离心率是（　　）
    A．$\frac{5}{4}$B．$\frac{5}{3}$C．$\frac{7}{3}$D．$\frac{\sqrt{21}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的右焦点F作x轴的垂线，交双曲线于A、B两点，若双曲线的左顶点C在以AB为直径的圆的内部，则此双曲线离心率e的取值范围是（　　）
    A．（$\frac{1+\sqrt{5}}{2}，+∞$）B．（$\frac{1+\sqrt{5}}{2}，2$）C．（2，+∞）D．（1，$\frac{1+\sqrt{5}}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上的一点，F1，F2是焦点，PF1与渐近线平行，∠F1PF2=90°，则双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．从重量分别为1，2，3，4，…，10，11克的砝码（每种砝码各一个）中选出若干个，使其总重量恰为9克的方法总数为m，下列各式的展开式中x9的系数为m的选项是（　　）
    A．（1+x）（1+x2）（1+x3）…（1+x11）
    B．（1+x）（1+2x）（1+3x）…（1+11x）
    C．（1+x）（1+2x2）（1+3x3）…（1+11x11）
    D．（1+x）（1+x+x2）（1+x+x2+x3）…（1+x+x2+…+x11）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直角梯形ABCD中，AD⊥AB，AB∥DC，AB=2，DC=3，E为AB的中点，将四边形AEFD沿EF折起使面AEFD⊥面EBCF，过E作EF∥AD，
    （1）若G为DF的中点，求证：EG∥面BCD；
    （2）若AD=2，试求多面体AD-BCFE体积．

    查看答案和解析>>

    同步练习册答案