
����Ŀ��Ϊ�˽�ijУ������ҵ����������רҵѧ�������أ���λ��ǧ�ˣ�����������ǵ���������������õ�����Ƶ�ʷֲ�ֱ��ͼ����֪ͼ�д�������ǰ3��С���Ƶ��֮��Ϊ1:2:3�����е�2С���Ƶ��Ϊ12.
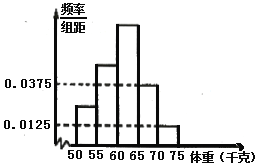
�������У��������רҵѧ����������![]() ��
��
������֪A�� ![]() �Ǹ�У��������רҵ������ѧ����A������С��55ǧ�ˣ�
�Ǹ�У��������רҵ������ѧ����A������С��55ǧ�ˣ� ![]() �����ز�С��70ǧ�ˣ��ִӸ�У��������רҵ��ѧ���а��ֲ�����ֱ��ȡ����С��55ǧ�˺Ͳ�С��70ǧ�˵�ѧ����6����Ȼ���ٴ���6���г�ȡ����С��55ǧ��ѧ��1�ˣ����ز�С��70ǧ�˵�ѧ��2�����3��ѵ���飬��A����ѵ������
�����ز�С��70ǧ�ˣ��ִӸ�У��������רҵ��ѧ���а��ֲ�����ֱ��ȡ����С��55ǧ�˺Ͳ�С��70ǧ�˵�ѧ����6����Ȼ���ٴ���6���г�ȡ����С��55ǧ��ѧ��1�ˣ����ز�С��70ǧ�˵�ѧ��2�����3��ѵ���飬��A����ѵ������![]() ��ѵ����ĸ���.
��ѵ����ĸ���.
���𰸡���1��![]() ��2��
��2��![]()
���������������������������Ƶ�ʷֲ�ֱ��ͼ��ʵ�����������⣻�������г����л����¼����ҳ����������Ļ����¼������ùŵ���͵ĸ��ʹ�ʽ�������.
�����������1�����У��������רҵ������Ϊn��ǰ��С���Ƶ��Ϊ![]() ����������ɵã�
����������ɵã� ![]() .����Ϊ
.����Ϊ![]() ����
����![]() .
.
��2�������⣬��������רҵ��ѧ���У�����С��55ǧ�˵�����Ϊ![]() �������Ƿֱ�Ϊ
�������Ƿֱ�Ϊ![]() ���ز�С��70ǧ�˵�����Ϊ
���ز�С��70ǧ�˵�����Ϊ![]() �������Ƿֱ�Ϊ
�������Ƿֱ�Ϊ![]() ��������С��55ǧ�˵�6���г�ȡ1�ˣ����ز�С��70ǧ�˵�3���г�ȡ2�����3��ѵ���飬���п��ܽ���У�(A,a,b)��(A,a,c)��(A,b,c)��(B,a,b)��(B,a,c)��(B,b,c)��(C,a,b)��(C,a,c)��(C,b,c)��(D,a,b)��(D,a,c)��(D,b,c)��(E,a,b)��(E,a,c)��(E,b,c)��(F,a,b)��(F,a,c)��(F,b,c)����18�֣�
��������С��55ǧ�˵�6���г�ȡ1�ˣ����ز�С��70ǧ�˵�3���г�ȡ2�����3��ѵ���飬���п��ܽ���У�(A,a,b)��(A,a,c)��(A,b,c)��(B,a,b)��(B,a,c)��(B,b,c)��(C,a,b)��(C,a,c)��(C,b,c)��(D,a,b)��(D,a,c)��(D,b,c)��(E,a,b)��(E,a,c)��(E,b,c)��(F,a,b)��(F,a,c)��(F,b,c)����18�֣�
����A����ѵ������a��ѵ����Ľ����(B,a,b)��(B,a,c)��(C,a,b)��(C,a,c)��(D,a,b)��(D,a,c)��(E,a,b)��(E,a,c)��(F,a,b)��(F,a,c)����10��.
�ʸ���Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲM��x2+��y-2��2=1��Q��x���ϵĶ��㣬QA��QB�ֱ���ԲM��A��B���㡣
��1����Q��1��0����������QA��QB�ķ��̣�
��2�����ı���QAMB�������Сֵ��
��3����|AB|=![]() ����ֱ��MQ�ķ��̡�
����ֱ��MQ�ķ��̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��![]() �У��ڽ�
�У��ڽ�![]() �Աߵı߳��ֱ���
�Աߵı߳��ֱ���![]() ����֪
����֪![]() ��
��![]() ��
��
��������![]() ���������
���������![]() ����
����![]() ��
��
��������![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
��
��1������![]() �����ֵ��
�����ֵ��
��2����������![]() ����
����![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ��ʹ
��ʹ![]() ��
��
���������������![]() �ķ�Χ���������ڣ�˵�����ɣ�
�ķ�Χ���������ڣ�˵�����ɣ�
��3������������![]() ����
����![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() �����ж�
�����ж�![]() ��
��![]()
�Ĵ�С��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ԭ��ΪO������P��x0��y0����ԲO��x2+y2=2�����ߣ��е�ΪQ�� ![]()
��1����|OP|��ֵ��
��2����֪��A��1��0����B��0��1������W��x��y�������� ![]() ���W�Ĺ켣���̣�
���W�Ĺ켣���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|+|x+5��a|
��1��������ʽf��x����|x��a|��2�Ľ⼯Ϊ[��5����1]����ʵ��a��ֵ��
��2����x0��R��ʹ��f��x0����4m+m2 �� ��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
(1)������![]() ���溯������ʵ��
���溯������ʵ��![]() ��ֵ��
��ֵ��
(2)��(1)�������£��жϺ���![]() �뺯��
�뺯��![]() ��ͼ�����������˵�����ɣ�
��ͼ�����������˵�����ɣ�
(3)��![]() ʱ������
ʱ������![]() ��ͼ��ʼ���ں���
��ͼ��ʼ���ں���![]() ��ͼ���Ϸ�����ʵ��
��ͼ���Ϸ�����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() �ķ���Ϊ��
�ķ���Ϊ��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
��1����֤��ֱ��![]() ������㣻
������㣻
��2����ֱ��![]() ��Բ
��Բ![]() �صõ��ҳ����ʱ����ֱ��
�صõ��ҳ����ʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
��3���ڣ�2����ǰ���£���![]() Ϊֱ��
Ϊֱ��![]() �ϵĶ��㣬��Բ
�ϵĶ��㣬��Բ![]() �ϴ���������ͬ�ĵ㵽��
�ϴ���������ͬ�ĵ㵽��![]() �ľ���Ϊ
�ľ���Ϊ![]() �����
�����![]() �ĺ������ȡֵ��Χ.
�ĺ������ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ�ϵĵ�A(2,3)����ֱ��x��2y��0�ĶԳƵ�����Բ�ϣ���ֱ��x��y��1��0��Բ�صõ��ҳ�Ϊ2![]() ����Բ�ķ��̣�
����Բ�ķ��̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com