
【题目】某酱油厂对新品种酱油进行了定价,在各超市得到售价与销售量的数据如下表:
单价 | 5 | 5.2 | 5.4 | 5.6 | 5.8 | 6 |
销量 | 9.0 | 8.4 | 8.3 | 8.0 | 7.5 | 6.8 |
(1)求售价与销售量的回归直线方程;(![]() ,
,![]() )
)
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/瓶,为使工厂获得最大利润(利润=销售收入![]() 成本),该产品的单价应定为多少元?
成本),该产品的单价应定为多少元?
相关公式: ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,
且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)求证:PB//平面EAC;
(2)求证:AE⊥平面PCD;
(3)当![]() 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅游业作为一个第三产业,时间性和季节性非常强,每年11月份来临,全国各地就相继进入旅游淡季,很多旅游景区就变得门庭冷落.为改变这种局面,某旅游公司借助一自媒体平台做宣传推广,销售特惠旅游产品.该公司统计了活动刚推出一周内产品的销售数量,用![]() 表示活动推出的天数,用
表示活动推出的天数,用![]() 表示产品的销售数量(单位:百件),统计数据如下表所示.
表示产品的销售数量(单位:百件),统计数据如下表所示.
![]()

根据以上数据,绘制了如图所示的散点图,根据已有的函数知识,发现样本点分布在某一条指数型函数![]() 的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立
的周围.为求出该回归方程,相关人员确定的研究方案是:先用其中5个数据建立![]() 关于
关于![]() 的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
的回归方程,再用剩下的2组数据进行检验.试回答下列问题:
(1)现令![]() ,若选取的是
,若选取的是![]() 这5组数据,已知
这5组数据,已知![]() ,
,![]() ,请求出
,请求出![]() 关于
关于![]() 的线性回归方程(结果保留一位有效数字);
的线性回归方程(结果保留一位有效数字);
(2)若由回归方程得到的估计数据与选出的检验数据的误差均不超过![]() ,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
,则认为得到的回归方程是可靠的,试问(1)中所得的回归方程是否可靠?
参考公式及数据:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
, ![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为![]() 小时,其余工人加工完乙型装置所需时间为
小时,其余工人加工完乙型装置所需时间为![]() 小时,则生产1000台某产品的总加工时间y是一个关于x的函数。
小时,则生产1000台某产品的总加工时间y是一个关于x的函数。
(1)求y关于x的函数解析式;
(2)如何分配工人才能使生产1000台某产品的总加工时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山西省在2019年3月份的高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布![]() ,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
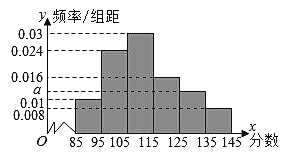
(1)求全市数学成绩在135分以上的人数;
(2)试由样本频率分布直方图佔计该校数学成绩的平均分数;
(3)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的一个顶点重合,且这个顶点与椭圆
的一个顶点重合,且这个顶点与椭圆![]() 的两个焦点构成的三角形面积为
的两个焦点构成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的上顶点为
的上顶点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,连接
为坐标原点,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1).在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).

(1)求证:![]() 平面
平面![]() ;
;
(2)当点![]() 在何处时,三棱锥
在何处时,三棱锥![]() 体积最大,并求出最大值;
体积最大,并求出最大值;
(3)当三棱锥![]() 体积最大时,求
体积最大时,求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com