
【题目】已知函数![]() 有两个零点
有两个零点![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() , 对于符合题意的任意
, 对于符合题意的任意![]() ,当
,当![]() 时均有
时均有![]() ?
?
若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先分离得![]() ,再利用导数可得
,再利用导数可得![]() 单调性:先减再增,结合图像以及值域可得
单调性:先减再增,结合图像以及值域可得![]() 的取值范围;(2)先根据
的取值范围;(2)先根据![]() ,得
,得![]() ,再根据零点解得
,再根据零点解得![]() ,转化不等式得
,转化不等式得![]() ,令
,令![]() ,化简得
,化简得![]() ,因此
,因此![]() ,
, ![]() ,最后根据导数研究对应函数单调性,确定对应函数最值,即得
,最后根据导数研究对应函数单调性,确定对应函数最值,即得![]() 取值集合
取值集合
试题解析:(1) ![]() ,
,
当![]() 时,
时, ![]() 对
对![]() 恒成立,与题意不符,
恒成立,与题意不符,
当![]() ,
, ![]() ,
,
∴![]() 时
时![]() ,
,
即函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
∵![]() 和
和![]() 时均有
时均有![]() ,
,
∴![]() ,解得:
,解得: ![]() ,
,
综上可知: ![]() 的取值范围
的取值范围![]() ;
;
(2)由(1)可知![]() ,
,
由![]() 的任意性及
的任意性及![]() 知,
知, ![]() ,且
,且![]() ,
,
![]() ∴
∴![]() ,
,
故![]() ,
,
又∵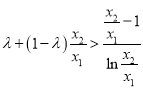 ,令
,令![]() ,则
,则![]() ,且
,且![]() 恒成立,
恒成立,
令![]() ,而
,而![]() ,
,
∴![]() 时,
时, ![]() 时,
时, ![]()
∴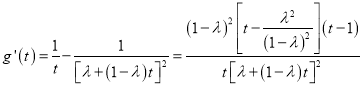 ,令
,令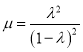 ,
,
若![]() ,则
,则![]() 时,
时, ![]() ,即函数在
,即函数在![]() 单调递减,
单调递减,
∴![]() ,与
,与![]() 不符;
不符;
若![]() ,则
,则![]() 时,
时, ![]() ,即函数
,即函数![]() 在
在![]() 单调递减,
单调递减,
∴![]() ,与
,与![]() 式不符;
式不符;
若![]() ,解得
,解得![]() ,此时
,此时![]() 恒成立,
恒成立, ![]() ,
,
即函数![]() 在
在![]() 单调递增,又
单调递增,又![]() ,
,
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() 符合
符合![]() 式,
式,
综上,存在唯一实数![]() 符合题意.
符合题意.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】先后抛掷两枚骰子,设出现的点数之和是12,11,10的概率依次是P1,P2,P3,则( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 是棱长为2的正方体
是棱长为2的正方体![]() 的棱
的棱![]() 的中点,点
的中点,点![]() 在面
在面![]() 所在的平面内,若平面
所在的平面内,若平面![]() 分别与平面
分别与平面![]() 和平面
和平面![]() 所成的锐二面角相等,则点
所成的锐二面角相等,则点![]() 到点
到点![]() 的最短距离是( )
的最短距离是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本
万元(总成本![]() 固定成本
固定成本![]() 生产成本).销售收入
生产成本).销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入
销售收入![]() 总成本);
总成本);
(2)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
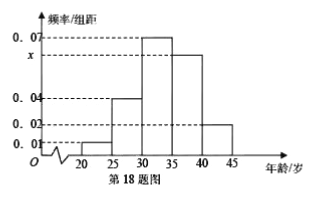
【题目】为增强市民的节能环保意识,汕头市面向全市征召义务宣传志愿者,从符合条件的 500 名志愿者中随机抽取 100 名,其年龄频率分布直方图如图所示,其中年龄分组区是:
![]() ,
,
(1)求图中![]() 的值,并根据频率分布直方图估计这 500 名志愿者中年龄在
的值,并根据频率分布直方图估计这 500 名志愿者中年龄在![]() 岁的人数;
岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 10 名参加人民广场的宣传活动,再从这 10 名志愿者中选取 3 名担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 ![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题![]() “
“![]() ”,则
”,则![]() :“
:“![]() ”
”
B. 命题“若![]() ,则
,则![]() ”的否命题是真命题
”的否命题是真命题
C. 若![]() 为假命题,则
为假命题,则![]() 为假命题
为假命题
D. 若![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需要看不同类型的书籍,为了合理配备资源,现对小区看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图,问:
后得到如图所示的频率分布直方图,问:
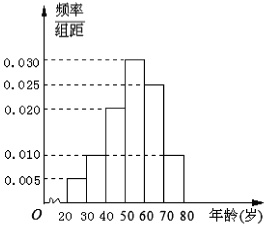
(1)在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)估计40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A. 若![]() 的观测值为
的观测值为![]() ,在犯错误的概率不超过
,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B. 由独立性检验可知,在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有![]() 的可能患有肺癌.
的可能患有肺癌.
C. 若从统计量中求出在犯错误的概率不超过![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D. 以上三种说法都不正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com