
����Ŀ��ij��˾ÿ����������λ���������ܹ�˾��λ�ڽ����ķֹ�˾��һ�����صİ��ÿ�갴200�������ռ��㣩����������ʹ�ð�ķ���������һ�ǹ���һ����ͣ��軨��90��Ԫ��������Ϊ10�꣬����ƽ��ÿ��ĸ��ַ��úϼ�5��Ԫ��˾���깤��6��Ԫ��˾��ÿ����ٵĸ���Ϊ0.1��ÿ�����ʱ�䲻����15�첻�۹��ʣ�����15��ÿ��100Ԫ������˾���������ӹ�����˾��Ӷ˾����ÿ��֧��300Ԫ����.�����������ù�����˾�ij�������˾���������ݵ���ÿ��12���µij�������ָ����ֱ��ͼ��ʾ�����е�ij�³�������ָ����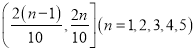 ʱ�������Ϊ
ʱ�������Ϊ![]() ��Ԫ.
��Ԫ.
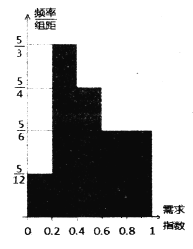
��1���������ͣ���˾��ÿ���������Ϊ![]() ����˾��˾����ٶ����ӵĻ���
����˾��˾����ٶ����ӵĻ���![]() ��Ԫ����ʹ�ð��ƽ������
��Ԫ����ʹ�ð��ƽ������![]() ����Ԫ������ѧ����
����Ԫ������ѧ����![]() .
.
��2�����õ������ݣ�������˾ʹ�ð�Ľ��飬ʹ����ƽ����������.
���𰸡���1��![]() ����Ԫ����2��Ӧ��ʹ�÷�����
����Ԫ����2��Ӧ��ʹ�÷�����
�������������������1��˾��ÿ����ٵĸ���Ϊ0.1�������������![]() ���������ÿ��9��Ԫ��ÿ�공��5��Ԫ��ÿ�깤��6��Ԫ����ٳ���5�죬�������ӹ���
���������ÿ��9��Ԫ��ÿ�공��5��Ԫ��ÿ�깤��6��Ԫ����ٳ���5�죬�������ӹ���![]() ��Ԫ��2�����·ֱ�����ã������ͣ��루1���Ƚϵý���
��Ԫ��2�����·ֱ�����ã������ͣ��루1���Ƚϵý���
����������⣺������֪����![]() ʱ��
ʱ�� ![]() ��
��
��![]() ʱ��
ʱ�� ![]()
����![]()
����֪![]() ������
������![]()
����![]() ����Ԫ��
����Ԫ��
����ʹ�÷�����������֪ÿ�������Ϊ1.2��Ԫ���·�Ϊ![]()
ÿ�������Ϊ1.4��Ԫ���·�Ϊ![]() ��
��
ÿ�������Ϊ1.6��Ԫ���·�Ϊ![]() ��
��
ÿ�������Ϊ1.8��Ԫ���·�Ϊ![]() ��
��
ÿ�������Ϊ2��Ԫ���·�Ϊ![]() ��
��
���Է�����ÿ���ƽ������Ϊ![]() ��Ԫ
��Ԫ
����Ӧ��ʹ�÷�����������ʹ����ƽ����������


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x2��ax��1��x��[��5��5]
x2��ax��1��x��[��5��5]
��1����a=2������f��x�������ֵ����Сֵ��
��2��������f��x���ڶ��������ǵ�����������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=loga��x+1����g��x��=loga��1��x�����У�a��0��a��1����
��1������f��x��+g��x���Ķ�����
��2���ж�f��x��+g��x������ż�ԣ���˵�����ɣ�
��3����ʹf��x����g��x����0������x�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x�����㣺f��x+1��= ![]() ����x�ʣ�0��1]ʱ��f��x��=2x �� ��f��log29������ ��
����x�ʣ�0��1]ʱ��f��x��=2x �� ��f��log29������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() Ϊ�溯����
Ϊ�溯����
��1����ʵ��a��ֵ��
��2�����жϺ����ĵ����Բ�����֤����
��3���������x��R������ʽf��x����m���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��= ![]() +lg��1+3x���Ķ������ǣ� ��
+lg��1+3x���Ķ������ǣ� ��
A.�����ޣ��� ![]() ��?
��?
B.���� ![]() ��
�� ![]() ���ȣ�
���ȣ� ![]() ��+�ޣ�?
��+�ޣ�?
C.�� ![]() ��+�ޣ�?
��+�ޣ�?
D.�� ![]() ��
�� ![]() ���ȣ�
���ȣ� ![]() ��+�ޣ�
��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ���ѷ���f��x��=x�ĸ�����С�����˳�����г�һ�����У�������е�ͨ�ʽΪ�� ��
���ѷ���f��x��=x�ĸ�����С�����˳�����г�һ�����У�������е�ͨ�ʽΪ�� ��
A.![]() ��n��N*��
��n��N*��
B.an=n��n��1����n��N*��
C.an=n��1��n��N*��
D.an=2n��2��n��N*��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��E��������ABCD����ƽ����һ�㣬E����ABCD�ϵ���ͶӰFǡ��AC�ϣ�FG��BC��AB=AE=2����EAB=60�㣬�������ĸ����⣺
��1��CD����GEF��
��2��AG=1��
��3����AC��AE��Ϊ�ڱߵ�ƽ���ı��������8��
��4����EAD=60�㣮
������ȷ����ĸ���Ϊ�� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪0��a��1������f��x��=loga��ax��1��
��I������f��x���Ķ�����
�����ж�f��x���ĵ����ԣ�
������m����f��1��m����f��1��m2������m�ķ�Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com