已知⊙O1的极坐标方程为ρ=4cosθ.点A的极坐标是(2,π).
(Ⅰ)把⊙O1的极坐标方程化为直角坐标参数方程,把点A的极坐标化为直角坐标.
(Ⅱ)点M(x0,y0)在⊙O1上运动,点P(x,y)是线段AM的中点,求点P运动轨迹的直角坐标方程.
解:(I)∴⊙O
1的极坐标方程为ρ=4cosθ,∴两边者乘以ρ,得ρ
2=4ρcosθ
∵ρcosθ=x,ρsinθ=y,ρ
2=x
2+y
2,
∴⊙O
1的直角坐标方程为x
2+y
2=4x,化成标准方程得(x-2)
2+y
2=4
令x=2+2cosα,y=2sinα,得⊙O
1的参数方程为
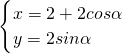
(α为参数)
设点A的直角坐标为(m,n)
∵点A的极坐标是(2,π),∴m=2cosπ=-2,n=2sinπ=0
由此可得点A的直角坐标为(-2,0).
(II)∵A(-2,0),M(x
0,y
0),
∴线段AM的中点P(x,y)满足

,可得
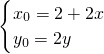
∵点M(x
0,y
0)在⊙O
1上运动,
∴(x
0-2)
2+y
02=4,可得[(2+2x)-2]
2+(2y)
2=4,化简得x
2+y
2=1
由此可得:点P运动轨迹的直角坐标方程为x
2+y
2=1.
分析:(I)将⊙O
1的极坐标方程两边者乘以ρ,得ρ
2=4ρcosθ,再根据公式ρcosθ=x和ρ
2=x
2+y
2,代入化简即可得到⊙O
1的直角坐标方程,进而得到⊙O
1的参数方程.最后由极坐标化直角坐标的公式,不难得到点A(2,π)的直角坐标.
(II)根据中点坐标公式和A、M的坐标,算出
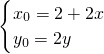
,再根据点M(x
0,y
0)是⊙O
1上的点,代入得到关于x、y二次方程,化简得x
2+y
2=1即为点P运动轨迹的直角坐标方程.
点评:本题给出⊙O
1的极坐标方程,求它的直角坐标方程与参数方程,并依此求动点P的轨迹.着重考查了极坐标方程与直角坐标方程、参数方程的互化和轨迹方程求法的一般步骤等知识,属于中档题.

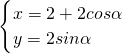 (α为参数)
(α为参数) ,可得
,可得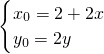
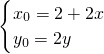 ,再根据点M(x0,y0)是⊙O1上的点,代入得到关于x、y二次方程,化简得x2+y2=1即为点P运动轨迹的直角坐标方程.
,再根据点M(x0,y0)是⊙O1上的点,代入得到关于x、y二次方程,化简得x2+y2=1即为点P运动轨迹的直角坐标方程.

 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案