
【题目】已知函数 ![]() 有两个极值点x1 , x2 , 其中b为常数,e为自然对数的底数.
有两个极值点x1 , x2 , 其中b为常数,e为自然对数的底数.
(1)求实数b的取值范围;
(2)证明:x1+x2>2.
【答案】
(1)解:函数f(x)的定义域为R,f'(x)=x+bex.
因为函数f(x)有两个极值点x1,x2,所以f'(x)=x+bex有两个变号零点,
故关于x的方程 ![]() 有两个不同的解,
有两个不同的解,
令 ![]() ,则
,则 ![]() ,
,
当x∈(﹣∞,1)时g'(x)>0,当x∈(1,+∞)时,g'(x)<0,
所以函数 ![]() 在区间(﹣∞,1)上单调递增,在区间(1,+∞)上单调递减,
在区间(﹣∞,1)上单调递增,在区间(1,+∞)上单调递减,
又当x→﹣∞时,g(x)→﹣∞;当x→+∞时,g(x)→0,且 ![]() ,
,
故 ![]() ,所以
,所以 ![]()
(2)解:不妨设x1<x2,由(1)可知,x1<1<x2,所以x1,2﹣x2∈(﹣∞,1),
因为函数 ![]() 在区间(﹣∞,1)上单调递增,
在区间(﹣∞,1)上单调递增,
若x1+x2>2即x1>2﹣x2时,g(x1)>g(2﹣x2)即g(x1)﹣g(2﹣x2)>0.
又g(x1)=g(x2),所以g(x1)﹣g(2﹣x2)>0可化为g(x2)﹣g(2﹣x2)>0,
即 ![]() 即
即 ![]() ,
,
令h(t)=e2t﹣e2t(2﹣t),则h(1)=0,h'(t)=e2﹣e2t(3﹣2t),
令φ(t)=h'(t),则φ(1)=0,φ'(t)=4e2t(t﹣1),
当t>1时,φ'(t)>0,所以h'(x)在区间(1,+∞)上单调递增,则h'(t)>h'(1)=0,
所以h(t)在区间(1,+∞)上单调递增,h(t)>h(1)=0.证毕
【解析】(1)求出函数的导数,问题转化为关于x的方程 ![]() 有两个不同的解,令
有两个不同的解,令 ![]() ,则
,则 ![]() ,根据函数的单调性求出b的范围即可;(2)问题转化为g(x2)﹣g(2﹣x2)>0,即
,根据函数的单调性求出b的范围即可;(2)问题转化为g(x2)﹣g(2﹣x2)>0,即 ![]() ,令h(t)=e2t﹣e2t(2﹣t),根据函数的单调性得到h(t)>0,从而证出结论.
,令h(t)=e2t﹣e2t(2﹣t),根据函数的单调性得到h(t)>0,从而证出结论.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点. 
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求AD与平面ABE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为
的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为 ![]() 时,AF2与x轴垂直. (I)求椭圆C的方程;
时,AF2与x轴垂直. (I)求椭圆C的方程;
(Ⅱ)在x轴上是否存在定点M,总能使MF1平分∠AMB?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表: 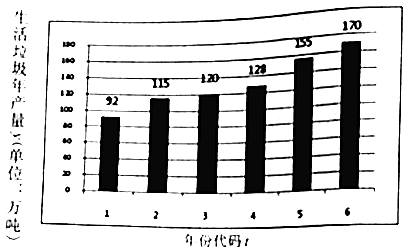
2016年初 | 2016年末 | |
社区A | 539 | 568 |
社区B | 543 | 585 |
社区C | 568 | 600 |
社区D | 496 | 513 |
注1:年份代码1~6分别对应年份2011~2016
注2:参与度= ![]() ×100%
×100%
参与度的年增加值=年末参与度﹣年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为 ![]() =14.8t+
=14.8t+ ![]() ,预测2020年该年生活垃圾的产生量;
,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题: ①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( ) 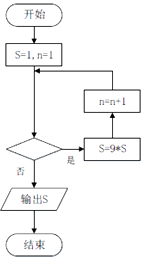
A.S>10000?
B.S<10000?
C.n≥5
D.n≤6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班开展一次智力竞赛活动,共a,b,c三个问题,其中题a满分是20分,题b,c满分都是25分.每道题或者得满分,或者得0分.活动结果显示,全班同学每人至少答对一道题,有1名同学答对全部三道题,有15名同学答对其中两道题.答对题a与题b的人数之和为29,答对题a与题c的人数之和为25,答对题b与题c的人数之和为20.则该班同学中只答对一道题的人数是;该班的平均成绩是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”). 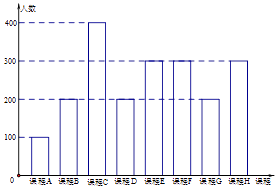
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组M”中选择F课程或G课程的同学,并且这些同学以自愿报名缴费的方式参加活动.选择F课程的学生中有x人参加科学营活动,每人需缴纳2000元,选择G课程的学生中有y人参加该活动,每人需缴纳1000元.记选择F课程和G课程的学生自愿报名人数的情况为(x,y),参加活动的学生缴纳费用总和为S元.
(ⅰ)当S=4000时,写出(x,y)的所有可能取值;
(ⅱ)若选择G课程的同学都参加科学营活动,求S>4500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若直线g(x)=ax+b是函数f(x)=lnx﹣ ![]() 图象的切线,求a+b的最小值;
图象的切线,求a+b的最小值;
(3)当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .
(取e为2.8,取ln2为0.7,取 ![]() 为1.4)
为1.4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com