
分析 (1)根据极坐标和普通坐标之间的关系$\left\{\begin{array}{l}ρsinθ=y\\ ρcosθ=x\end{array}\right.$进行转化求解.
(2)将直线的参数方程代入抛物线方程,利用参数方程的几何意义进行求解.
解答 解:( 1)∵ρsin2θ-6cosθ=0,
∴ρ2sin2θ-ρ6cosθ=0,
由$\left\{\begin{array}{l}ρsinθ=y\\ ρcosθ=x\end{array}\right.$得y2=6x,即C的直角坐标方程,
直线l消去参数t得x=3+$\frac{\sqrt{3}}{2}$(2y),
整理得$x-\sqrt{3}y-3=0$.
(2)将l的参数方程代入y2=6x,得${t^2}-12\sqrt{3}t-72=0$.
设P1,P2对应参数分别为t1,t2,${t_1}+{t_2}=12\sqrt{3}$,t1•t2=-72,
所求$|{|{P_0}{P_1}|-|{P_0}{P_2}|}|=|{|{t_1}|-|{t_2}|}|=|{{t_1}+{t_2}}|=12\sqrt{3}$.
点评 本题主要考查参数方程,极坐标方程和普通方程之间的关系,根据相应的转化公式进行化简是解决本题的关键.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:选择题
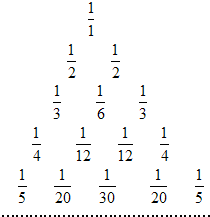 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$,$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$,$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$,…,| A. | $\frac{1}{2016×2015×2014}$ | B. | $\frac{1}{2016×2017}$ | C. | $\frac{1}{2016×2015×1006}$ | D. | $\frac{1}{2016×2015×1007}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方形的中心,P是平面 ABCD 外一点,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
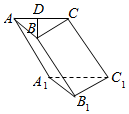 如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)
如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,已知AB是圆O的直径,点C,D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=( )
如图所示,已知AB是圆O的直径,点C,D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=( )| A. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com