
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P(1,0)的直线(不与坐标轴垂直)与椭圆交于A、B两点,设点B关于x轴的对称点为B'.直线AB'与x轴的交点Q是否为定点?请说明理由.
【答案】解:(Ⅰ)因为点(2,0)在椭圆C上,所以a=2. 又因为 ![]() ,所以
,所以 ![]() .
.
所以 ![]() .
.
所以椭圆C的标准方程为: ![]() .
.
(Ⅱ)设A(x1 , y1),B(x2 , y2),B'(x2 , ﹣y2),Q(n,0).
设直线AB:y=k(x﹣1)(k≠0).
联立y=k(x﹣1)和x2+4y2﹣4=0,得:(1+4k2)x2﹣8k2x+4k2﹣4=0.
所以 ![]() ,
, ![]() .
.
直线AB'的方程为 ![]() ,
,
令y=0,解得 ![]()
又y1=k(x1﹣1),y2=k(x2﹣1),
所以 ![]() .
.
所以直线AB'与x轴的交点Q是定点,坐标为Q(4,0)
【解析】(Ⅰ)由点(2,0)在椭圆C上,可得a=2,又 ![]() ,b=
,b= ![]() ,解出即可得出.(Ⅱ)设A(x1 , y1),B(x2 , y2),B'(x2 , ﹣y2),Q(n,0).设直线AB:y=k(x﹣1)(k≠0).与椭圆方程联立得:(1+4k2)x2﹣8k2x+4k2﹣4=0.直线AB'的方程为
,解出即可得出.(Ⅱ)设A(x1 , y1),B(x2 , y2),B'(x2 , ﹣y2),Q(n,0).设直线AB:y=k(x﹣1)(k≠0).与椭圆方程联立得:(1+4k2)x2﹣8k2x+4k2﹣4=0.直线AB'的方程为 ![]() ,令y=0,解得n,又y1=k(x1﹣1),y2=k(x2﹣1),再利用根与系数的关系即可得出.
,令y=0,解得n,又y1=k(x1﹣1),y2=k(x2﹣1),再利用根与系数的关系即可得出.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】如图长方体ABCD﹣A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
(Ⅰ)求证:FG∥面ADD1A1;
(Ⅱ)求二面角B﹣EF﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟定2016年城市建设A,B,C三项重点工程,该市一大型城建公司准备参加这三个工程的竞标,假设这三个工程竞标成功与否相互独立,该公司对A,B,C三项重点工程竞标成功的概率分别为a,b, ![]() (a>b),已知三项工程都竞标成功的概率为
(a>b),已知三项工程都竞标成功的概率为 ![]() ,至少有一项工程竞标成功的概率为
,至少有一项工程竞标成功的概率为 ![]() .
.
(1)求a与b的值;
(2)公司准备对该公司参加A,B,C三个项目的竞标团队进行奖励,A项目竞标成功奖励2万元,B项目竞标成功奖励4万元,C项目竞标成功奖励6万元,求竞标团队获得奖励金额的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国唐代诗人王维诗云:“明月松间照,清泉石上流”,这里明月和清泉,都是自然景物,没有变,形容词“明”对“清”,名词“月”对“泉”,词性不变,其余各词均如此.变化中的不变性质,在文学和数学中都广泛存在.比如我们利用几何画板软件作出抛物线C:x2=y的图象(如图),过交点F作直线l交C于A、B两点,过A、B分别作C的切线,两切线交于点P,过点P作x轴的垂线交C于点N,拖动点B在C上运动,会发现 ![]() 是一个定值,该定值是 .
是一个定值,该定值是 . 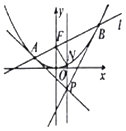
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C: ![]() =1,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ﹣2sinθ)=6.
=1,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ﹣2sinθ)=6.
(Ⅰ)写出直线l的直角坐标方程和曲线C的参数方程;
(Ⅱ)在曲线C上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n(3≤m≤n)是正整数,数列Am:a1 , a2 , …,am , 其中ai(1≤i≤m)是集合{1,2,3,…,n}中互不相同的元素.若数列Am满足:只要存在i,j(1≤i<j≤m)使ai+aj≤n,总存在k(1≤k≤m)有ai+aj=ak , 则称数列Am是“好数列”. (Ⅰ)当m=6,n=100时,
(ⅰ)若数列A6:11,78,x,y,97,90是一个“好数列”,试写出x,y的值,并判断数列:11,78,90,x,97,y是否是一个“好数列”?
(ⅱ)若数列A6:11,78,a,b,c,d是“好数列”,且a<b<c<d,求a,b,c,d共有多少种不同的取值?
(Ⅱ)若数列Am是“好数列”,且m是偶数,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在y轴上的椭圆E的中心是原点O,离心率等于 ![]() ,以椭圆E的长轴和短轴为对角线的四边形的周长为4
,以椭圆E的长轴和短轴为对角线的四边形的周长为4 ![]() ,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
,直线,l:y=kx+m与y轴交干点P,与椭圆E相交于A、B两个点. (Ⅰ)求椭圆E的方程;
(Ⅱ)若 ![]() =3
=3 ![]() ,求m2的取值范围.
,求m2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com