
【题目】![]() . 问:是否存在正数m,使得对于任意正数
. 问:是否存在正数m,使得对于任意正数![]() ,可使
,可使![]() 为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
为三角形的三边构成三角形?如果存在:①试写出一组x,y,m的值,②求出所有m的值;如果不存在,请说明理由.
【答案】![]()
【解析】试题分析:首先判断a>b,由构成三角形的条件可得b+c>a且a+b>c,即有![]() +m
+m![]() >x+y且x+y+
>x+y且x+y+![]() >m
>m![]() .运用参数分离和换元法,结合基本不等式和函数的单调性,可得最值,进而得到m的范围.
.运用参数分离和换元法,结合基本不等式和函数的单调性,可得最值,进而得到m的范围.
试题解析:
x>0,y>0,a=x+y,![]() ,
,![]() ,
,
由a2﹣b2=(x+y)2﹣(x2+xy+y2)=xy>0,
可得a>b,
由题意可得要构成三角形,必须
b+c>a且a+b>c,
即有![]() +m
+m![]() >x+y
>x+y
且x+y+![]() >m
>m![]() .
.
由m<![]() ,
,
![]() ≥
≥![]() =2+
=2+![]() ,
,
当且仅当x=y取得等号.
可得m<2+![]() ①
①
由m>![]() ,
,
![]() =
=![]() +
+![]() ﹣
﹣![]() ,
,
令u=![]() ,则上式为u+
,则上式为u+![]() ﹣
﹣![]() .
.
可令t=u+![]() (t≥2),可得上式为t﹣
(t≥2),可得上式为t﹣![]() =
=![]() ,
,
可得在[2,+∞)递减,可得t﹣![]() ≤2﹣
≤2﹣![]() ,
,
即有m>2﹣![]() ②
②
由①②可得m的取值范围是(2﹣![]() ,2+
,2+![]() ).
).


科目:高中数学 来源: 题型:
【题目】在![]() 中,已知(sin A+sin B+sin C)·(sin B+sin C-sin A)=3sin Bsin C.
中,已知(sin A+sin B+sin C)·(sin B+sin C-sin A)=3sin Bsin C.
(Ⅰ)求角A的值;
(Ⅱ)求![]() sin B-cos C的最大值.
sin B-cos C的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
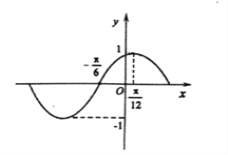
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①对任意的α∈R都有sin3α=3sinα﹣4sin3α成立;
②对任意的△ABC都有等式a=bcosA+ccosB成立;
③满足“三边是连续的三个正整数且最大角是最小的2倍”的三角形存在且唯一;
④若A,B是钝角△ABC的二锐角,则sinA+sinB<cosA+cosB.
其中正确的命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com