
【题目】已知函数f(x)=|x﹣2|+|x+1|.
(1)解关于x的不等式f(x)≤5;
(2)若函数f(x)的最小值记为m,设a,b,c均为正实数,且a+4b+9c=m,求![]() 的最小值.
的最小值.
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点F且倾斜角为
的焦点F且倾斜角为![]() 的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
的直线交抛物线于AB两点,交其准线于点C,且|AF|=|FC|,|BC|=2.
(1)求抛物线C的方程;
(2)直线l交抛物线C于DE两点,且这两点位于x轴两侧,与x轴交于点M,若![]() ·
·![]() 求
求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差![]() 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时![]() 的值.
的值.
(注:![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点S为正方形ABCD所在平面外一点,△SBC是边长为2的等边三角形,点E为线段SB的中点.
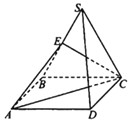
(1)证明:SD//平面AEC;
(2)若侧面SBC⊥底面ABCD,求平面ACE与平面SCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如图:

每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;
(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为其左顶点,点
为其左顶点,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,当
两点,当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .
.
(1)求该椭圆的方程;
(2)设直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,设直线
,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标点xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=6.
(1)A为曲线C1上的动点,点M在线段OA上,且满足|OM||OA|=36,求点M的轨迹C2的直角坐标方程;
(2)点E的极坐标为(4,![]() ),点F在曲线C2上,求△OEF面积的最大值
),点F在曲线C2上,求△OEF面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com