
分析 (1)由图象经过点A(1,$\frac{1}{2}$),B(3,2)可得ba=$\frac{1}{2}$,ba3=2,联立解方程组可得;
(2)令t=($\frac{1}{2}$)x,二次函数区间的最值求y=t2-t+1,t∈[$\frac{1}{4}$,8]值域可得E,再由指数的运算化简可得λ,可得答案.
解答 解:(1)∵函数f(x)=b•ax(a>0且a≠1,b∈R)的图象经过点A(1,$\frac{1}{2}$),B(3,2),
∴ba=$\frac{1}{2}$,ba3=2,联立解得a=2,b=$\frac{1}{4}$,
故f(x)的解析式为f(x)=$\frac{1}{4}$•2x=2x-2;
(2)由(1)可得y=bx-($\frac{1}{a}$)x+1=($\frac{1}{4}$)x-($\frac{1}{2}$)x+1=[($\frac{1}{2}$)x]2-($\frac{1}{2}$)x+1,
令t=($\frac{1}{2}$)x,由x∈[-3,2]可得t∈[$\frac{1}{4}$,8],故y=t2-t+1,t∈[$\frac{1}{4}$,8],
由二次函数可知当t=$\frac{1}{2}$时,y取最小值$\frac{3}{4}$,当t=8时,y取最大值57,
故E=[$\frac{3}{4}$,57],
化简可得λ=($\frac{1}{10}$)0+${8^{-\frac{2}{3}}}$+$\root{3}{{{{(-\frac{3}{4})}^3}}}$=1+$\frac{1}{4}$-$\frac{3}{4}$=$\frac{3}{2}$,
故λ与E关系为λ∈E.
点评 本题考查函数解析式求解方法,涉及换元法和二次函数区间的最值,属中档题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
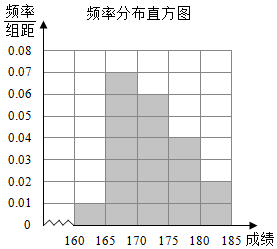 某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示
某高校在2015年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4项 | B. | 5项 | C. | 6项 | D. | 7项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com