
 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年) .(设该生物出生时t=0)
.(设该生物出生时t=0) 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值. ,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求
,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求 的最大值,即
的最大值,即 就是这个最大值,下面我们只要求出
就是这个最大值,下面我们只要求出 ,分析它的最大值是在
,分析它的最大值是在 为何值时取得,
为何值时取得,
 ,此式较繁,因此我们用换元法,设
,此式较繁,因此我们用换元法,设 ,由有
,由有

 ,它的最大值求法一般是分子分母同时除以
,它的最大值求法一般是分子分母同时除以 ,然后用基本不等式及不等式的性质得到结论.
,然后用基本不等式及不等式的性质得到结论. ,即
,即 ,解得
,解得 ,
,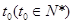 年生长最快,于是有
年生长最快,于是有 , 8分
, 8分 ,则
,则 ,
, , 11分
, 11分 即
即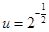 ,
, ,
, 时成立,因为
时成立,因为 ,因此
,因此 可能值为4或5,由
可能值为4或5,由 知,所求有年份为第4年和第5年,两年内各生长了
知,所求有年份为第4年和第5年,两年内各生长了 米. 14分
米. 14分

科目:高中数学 来源:不详 题型:单选题
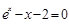 的一个根所在的区间是( )
的一个根所在的区间是( )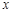 | -1 | 0 | 1 | 2 | 3 |
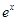 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
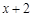 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com