练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知为坐标原点，椭圆的右焦点为，过的直线与相交于两点，点满足.

    （1）当的倾斜角为时，求直线的方程；

    （2）试探究在轴上是否存在定点，使得为定值？若存在，求出点的坐标；若不存在，请说明理由.

    【答案】（1）；（2）在轴上是否存在定点，，使得为定值．

    【解析】

    （1）联立直线与椭圆方程求出，，进而可求的的坐标，即可得到直线的方程；

    （2）假设，设直线的方程为，，，，，联立直线和椭圆方程得到韦达定理，再把韦达定理代入化简即得解.

    （1）椭圆的右焦点为，

    直线的方程为，

    由，解得或，

    不妨设，，，

    点满足．点，，

    则，所以直线的方程为．

    （2）假设，设直线的方程为，，，，，

    由，消可得，

    ，，

    ，，，

    ，

    ，

    ，

    当且仅当，即时，为定值．

    故在轴上是否存在定点，，使得为定值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列四个命题中，正确命题的个数有（ ）

    ①，

    ②命题“，”的否定是“，”

    ③“若，则，中至少有一个不小于2”的逆命题是真命题

    ④复数，则的充分不必要条件是

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥的底面是边长为2的正方形，平面平面，，．

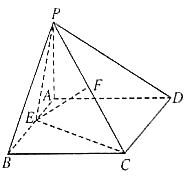
    （1）求证：平面平面；

    （2）设为的中点，问边上是否存在一点，使平面，并求此时点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某花卉企业引进了数百种不同品种的康乃馨，通过试验田培育，得到了这些康乃馨种子在当地环境下的发芽率，并按发芽率分为组：、、、加以统计，得到如图所示的频率分布直方图．企业对康乃馨的种子进行分级，将发芽率不低于的种子定为“级”，发芽率低于但不低于的种子定为“级”，发芽率低于的种子定为“级”．

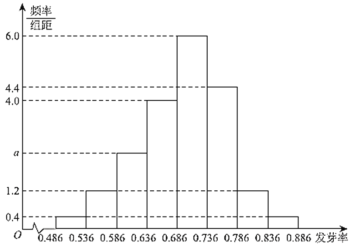
    （Ⅰ）现从这些康乃馨种子中随机抽取一种，估计该种子不是“级”种子的概率；

    （Ⅱ）该花卉企业销售花种，且每份“级”、“级”、“级”康乃馨种子的售价分别为元、元、元．某人在市场上随机购买了该企业销售的康乃馨种子两份，共花费元，以频率为概率，求的分布列和数学期望；

    （Ⅲ）企业改进了花卉培育技术，使得每种康乃馨种子的发芽率提高到原来的倍，那么对于这些康乃馨的种子，与旧的发芽率数据的方差相比，技术改进后发芽率数据的方差是否发生变化？若发生变化，是变大了还是变小了？（结论不需要证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某建材商场国庆期间搞促销活动，规定：如果顾客选购物品的总金额不超过600元，则不享受任何折扣优惠；如果顾客选购物品的总金额超过600元，则超过600元部分享受一定的折扣优惠，折扣优惠按下表累计计算.

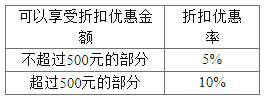
    某人在此商场购物获得的折扣优惠金额为30元，则他实际所付金额为____元．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：

    质量指标值分组

    [75，85)

    [85，95)

    [95，105)

    [105，115)

    [115，125)

    频数

    6

    26

    38

    22

    8

    （I）在答题卡上作出这些数据的频率分布直方图：

    （II）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；

    （III）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线在点处的切线方程是.

    （Ⅰ）求实数，的值;

    （Ⅱ）若函数有两个不同的零点，，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若抛物线的焦点为，是坐标原点，为抛物线上的一点，向量与轴正方向的夹角为60°，且的面积为.

    （1）求抛物线的方程；

    （2）若抛物线的准线与轴交于点，点在抛物线上，求当取得最大值时，直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知点，，抛物线的焦点为线段中点.

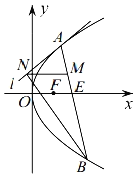
    （1）求抛物线的方程；

    （2）过点的直线交抛物线于两点，，过点作抛物线的切线，为切线上的点，且轴，求面积的最小值.

    查看答案和解析>>

    同步练习册答案