Question

已知等式x⁴=（x+1）⁴+b₁（x+1）³+b₂（x+1）²+b₃（x+1）+b₄，则b₁，b₂，b₃，b₄的值分别为（ ）
A．0，0，0，0
B．-4，6，-3，0
C．4，-6，4，-1
D．-4，6，-4，1

Answer 1

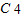
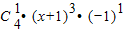
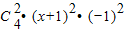
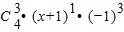
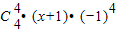
【答案】分析：由条件利用二项式定理可得x⁴=[（x+1）-1]⁴=•（X+1）⁴++++，再由已知 x⁴=（x+1）⁴+b₁（x+1）³+b₂（x+1）²+b₃（x+1）+b₄，由此可得 b₁，b₂，b₃，b₄的值．
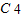
解答：解：由于x⁴=[（x+1）-1]⁴=•（X+1）⁴++
++，
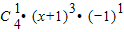
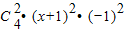
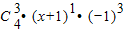
而且还有 x⁴=（x+1）⁴+b₁（x+1）³+b₂（x+1）²+b₃（x+1）+b₄，
则b₁=-4，b₂ =6，b₃ =-4，b₄=1，
故选D．
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．