
【题目】已知数列{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=![]() ,anbn+1+bn+1=nbn.
,anbn+1+bn+1=nbn.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
【答案】(1)an=3n-1,bn=![]() ,(2)Tn=
,(2)Tn= ![]() -
- ![]() (6n+7)31-n .
(6n+7)31-n .
【解析】
试题解析:(Ⅰ)∵anbn+1+bn+1=nbn.
当n=1时,a1b2+b2=b1.∵b1=1,b2=![]() , ∴a1=2,
, ∴a1=2,
又∵{an}是公差为3的等差数列, ∴an=3n-1,
∴![]() . 即
. 即![]() .
.
即数列{bn}是以1为首项,以![]() 为公比的等比数列, ∴bn=
为公比的等比数列, ∴bn=![]() ,
,
(Ⅱ)cn= an bn=(3n-1)![]()
∴Tn=2×![]() +5×
+5×![]() +8×
+8×![]() +……+(3n-1)
+……+(3n-1)![]() ①
①
![]() Tn= 2×
Tn= 2×![]() +5×
+5×![]() +8×
+8×![]() +……+(3n-1)
+……+(3n-1)![]() ②
②
① - ②:![]() Tn=2 +3×
Tn=2 +3×![]() +3×
+3×![]()
![]() -(3n-1)
-(3n-1)![]()
=2 + 3×![]() -(3n-1)
-(3n-1)![]()
∴Tn= ![]() -
- ![]() (6n+7)31-n .
(6n+7)31-n .


科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有一调查小组为了解本校学生假期中白天在家时间的情况,从全校学生中抽取![]() 人,统计他们平均每天在家的时间(在家时间在
人,统计他们平均每天在家的时间(在家时间在![]() 小时以上的就认为具有“宅”属性,否则就认为不具有“宅”属性)
小时以上的就认为具有“宅”属性,否则就认为不具有“宅”属性)
具有“宅”属性 | 不具有“宅”属性 | 总计 | |
男生 | 20 | 50 | 70 |
女生 | 10 | 40 | 50 |
总计 | 30 | 90 | 120 |
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过
列联表,并通过计算判断能否在犯错误的概率不超过
![]() 的前提下认为“是否具有‘宅’属性与性别有关?”
的前提下认为“是否具有‘宅’属性与性别有关?”
(2)采用分层抽样的方法从具有“宅”属性的学生里抽取一个![]() 人的样本,其中男生和女生各多少人?
人的样本,其中男生和女生各多少人?
从![]() 人中随机选取
人中随机选取![]() 人做进一步的调查,求选取的
人做进一步的调查,求选取的![]() 人至少有
人至少有![]() 名女生的概率.
名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 5.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 左、右焦点,点
左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的两个动点,如果直线
的两个动点,如果直线![]() 与直线
与直线![]() 的倾斜角互补,证明:直线
的倾斜角互补,证明:直线![]() 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
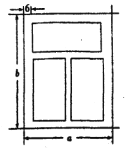
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com