
 如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=
如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=| a2011-2 | 2009 |
| n(n-1) |
| 2 |
| 2011×2010 |
| 2 |
| a2011-2 |
| 2009 |
| 1 |
| 2 |
| n(n-1) |
| 2 |
| 2011×2010 |
| 2 |
| a2011-2 |
| 2009 |
| 2021056-2 |
| 2009 |


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:2010-2011年安徽省马鞍山市高二下学期期中考试理科数学 题型:填空题
如图,数表满足;(1)第 行首尾两数均为
行首尾两数均为 ;(2)表中递推关系类似杨辉三角(即每一数是其上方相邻两数之和),记第
;(2)表中递推关系类似杨辉三角(即每一数是其上方相邻两数之和),记第 行第2个数为
行第2个数为 .根据表中上下两行数据关系,可以求得当
.根据表中上下两行数据关系,可以求得当 时,
时,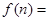 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=________,由此通过有关求解可以求得:
如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=________,由此通过有关求解可以求得: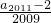 =________(用数字填写)
=________(用数字填写)查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市慈溪市高三(上)期中数学试卷(文科)(解析版) 题型:填空题
 = (用数字填写)
= (用数字填写)
查看答案和解析>>
科目:高中数学 来源: 题型:
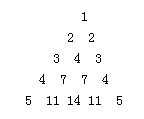 如图,数表满足;(1)第
如图,数表满足;(1)第![]() 行首尾两数均为
行首尾两数均为![]() ;(2)表中递推关系类似杨辉三角(即每一数是其上方相邻两数之和),记第
;(2)表中递推关系类似杨辉三角(即每一数是其上方相邻两数之和),记第![]() 行第2个数为
行第2个数为![]() .根据表中上下两行数据关系,可以求得当
.根据表中上下两行数据关系,可以求得当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com