
分析 (1)由题意可得B的坐标,然后得到椭圆左焦点的坐标,再利用椭圆定义求出2a,由隐含条件求得b,则椭圆方程可求;
(2)分CD所在直线斜率不存在和存在两种情况讨论,斜率不存在时求得三角形OCD面积,斜率存在时,设出直线方程y=kx+n,和椭圆方程联立,利用根与系数的关系结合OC⊥OD得到k与n的关系,由弦长公式求得弦长,由点到直线的距离公式求出原点O到直线l的距离,代入三角形面积公式,配方法利用函数单调性得到三角形OCD面积的范围得答案.
解答 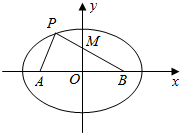 解:(1)如图,P(-1,$\frac{\sqrt{2}}{2}$).
解:(1)如图,P(-1,$\frac{\sqrt{2}}{2}$).
由题意可得:B(1,0),即c=1.
∴A(-1,0),则2a=|PA|+|PB|=$\sqrt{(-1+1)^{2}+(\frac{\sqrt{2}}{2}-0)^{2}}+\sqrt{(-1-1)^{2}+(\frac{\sqrt{2}}{2}-0)^{2}}$=$2\sqrt{2}$.
∴a2=2,b2=a2-c2=1.
则椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)当CD所在直线斜率不存在时,设直线方程为x=m,
联立$\left\{\begin{array}{l}{x=m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,解得C(m,$-\sqrt{1-\frac{{m}^{2}}{2}}$),D(m,$\sqrt{1-\frac{{m}^{2}}{2}}$).
由OC⊥OD,得${m}^{2}-(1-\frac{{m}^{2}}{2})=0$,解得m=$±\frac{\sqrt{6}}{3}$.
不妨取m=$\frac{\sqrt{6}}{3}$,则|CD|=$\frac{2\sqrt{6}}{3}$.
∴${S}_{△OCD}=\frac{1}{2}×\frac{2\sqrt{6}}{3}×\frac{\sqrt{6}}{3}=\frac{2}{3}$;
当CD所在直线斜率存在时,设直线l的方程为y=kx+n.
联立$\left\{\begin{array}{l}{y=kx+n}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2+4knx+2n2-2=0.
△=16k2n2-4(1+2k2)(2n2-2)=16k2-8n2+8.
设C(x1,y1),D(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{4kn}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{n}^{2}-2}{1+2{k}^{2}}$.
y1y2=(kx1+n)(kx2+n)=${k}^{2}{x}_{1}{x}_{2}+kn({x}_{1}+{x}_{2})+{n}^{2}$
=${k}^{2}•\frac{2{n}^{2}-2}{1+2{k}^{2}}+kn•(-\frac{4kn}{1+2{k}^{2}})+{n}^{2}$=$\frac{{n}^{2}-2{k}^{2}}{1+2{k}^{2}}$.
∵OC⊥OD,∴${x}_{1}{x}_{2}+{y}_{1}{y}_{2}=\frac{2{n}^{2}-2}{1+2{k}^{2}}+\frac{{n}^{2}-2{k}^{2}}{1+2{k}^{2}}$=$\frac{3{n}^{2}-2-2{k}^{2}}{1+2{k}^{2}}=0$.
∴3n2-2-2k2=0.
|CD|=$\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{(-\frac{4kn}{1+2{k}^{2}})^{2}-\frac{8{n}^{2}-8}{1+2{k}^{2}}}$
=$\sqrt{1+{k}^{2}}\frac{2\sqrt{2}\sqrt{2{k}^{2}-{n}^{2}+1}}{1+2{k}^{2}}$.
把3n2-2-2k2=0代入得:|CD|=$\frac{2\sqrt{6}}{3}\frac{\sqrt{(1+{k}^{2})(1+4{k}^{2})}}{1+2{k}^{2}}$.
原点O到直线l的距离d=$\frac{|n|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{6}}{3}$.
∴${S}_{△OCD}=\frac{1}{2}×\frac{\sqrt{6}}{3}×\frac{2\sqrt{6}}{3}\sqrt{\frac{4{k}^{4}+5{k}^{2}+1}{2{k}^{2}+1}}$=$\frac{2}{3}\sqrt{\frac{(2{k}^{2}+1)^{2}+\frac{1}{2}(2{k}^{2}+1)-\frac{1}{2}}{2{k}^{2}+1}}$
=$\frac{2}{3}\sqrt{(2{k}^{2}+1)-\frac{1}{2(2{k}^{2}+1)}+\frac{1}{2}}$.
∵1+2k2>1,∴$\sqrt{(2{k}^{2}+1)-\frac{1}{2{k}^{2}+1}+\frac{1}{2}}>1$.
则${S}_{△OCD}>\frac{2}{3}$.
综上,三角形OCD面积的最小值为$\frac{2}{3}$.
点评 本题考查利用椭圆定义求椭圆的标准方程,考查了椭圆的简单性质,体现了分类讨论的数学思想方法,考查计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
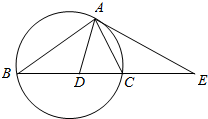 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com