
【题目】先将函数y=f(x)的图象向左平移 ![]() 个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,求函数y=g(x)在[0,
,2)对称,求函数y=g(x)在[0, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
【答案】解:(Ⅰ)由题意可得,把函数y=sinx的图象向下平移1个单位得y=sinx﹣1的图象,
然后再将y=sinx﹣1图象上所有点的纵坐标不变,横坐标缩短到原来的 ![]() 倍,得到y=sin2x﹣1的图象,
倍,得到y=sin2x﹣1的图象,
最后将函数y=sin2x﹣1的图象向右平移 ![]() 个单位得y=sin2(x﹣
个单位得y=sin2(x﹣ ![]() )﹣1的图象,
)﹣1的图象,
所以函数y=f(x)的表达式是y=sin(2x﹣ ![]() )﹣1.
)﹣1.
(Ⅱ)设函数y=f(x)=sin(2x﹣ ![]() )﹣1图象任意一点为P(m,n),点P(m,n)关于点M(
)﹣1图象任意一点为P(m,n),点P(m,n)关于点M( ![]() ,2)对称点为Q(x,y),
,2)对称点为Q(x,y),
由于函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,点Q(x,y)是函数y=g(x)图象上的点.
,2)对称,点Q(x,y)是函数y=g(x)图象上的点.
由中点坐标公式可得m+x= ![]() 且 n+y=4,即 m=
且 n+y=4,即 m= ![]() ﹣x且 n=4﹣y.
﹣x且 n=4﹣y.
由点P(m,n)在函数 y=sin(2x﹣ ![]() )﹣1的图象上,可得n=sin(2m﹣
)﹣1的图象上,可得n=sin(2m﹣ ![]() )﹣1,即有4﹣y=sin[2(
)﹣1,即有4﹣y=sin[2( ![]() ﹣x)﹣
﹣x)﹣ ![]() )]﹣1,
)]﹣1,
化简得y=sin(2x﹣ ![]() )+5,所以函数y=g(x)的解析式为y=sin(2x﹣
)+5,所以函数y=g(x)的解析式为y=sin(2x﹣ ![]() )+5.
)+5.
由于x∈[0, ![]() ],所以y=g(x)=sin(2x﹣
],所以y=g(x)=sin(2x﹣ ![]() )+5,根据2x﹣
)+5,根据2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],y=sin(2x﹣
],y=sin(2x﹣ ![]() )+5∈[4,5+
)+5∈[4,5+ ![]() ],
],
函数y=g(x)在[0, ![]() ]的最小值和最大值分别为4和5+
]的最小值和最大值分别为4和5+ ![]()
【解析】(Ⅰ)由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.(Ⅱ)由条件利用两个函数的图象关于某个点对称的性质,正弦函数的定义域和值域,求得函数y=g(x)在[0, ![]() ]的最小值和最大值.
]的最小值和最大值.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OAB是一块半径为1,圆心角为 ![]() 的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧
的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧 ![]() 上,记∠COA=θ.
上,记∠COA=θ.
(Ⅰ)写出矩形CDEF的面积S与角θ之间的函数关系式;
(Ⅱ)当角θ取何值时,矩形CDEF的面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,cosx),
=(cosx,cosx), ![]() =(sinx,﹣cosx),记函数f(x)=2
=(sinx,﹣cosx),记函数f(x)=2 ![]()
![]() +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函数f(x)的最小正周期及函数f(x)的图象的对称中心的坐标;
(Ⅱ)若α∈(0, ![]() ),且f(
),且f( ![]() )=
)= ![]() ,求cos2α的值.
,求cos2α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P的坐标为(x﹣3,y﹣2).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现在从盒子中随机取出一张卡片,记下标号后把卡片放回盒中,再从盒子中随机取出一张卡片记下标号,记先后两次抽取卡片的标号分别为x、y,求点P在第二象限的概率;
(2)若利用计算机随机在区间[0,3]上先后取两个数分别记为x、y,求点P在第三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中点..
,且M是BD的中点.. 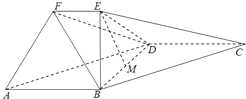
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com