
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
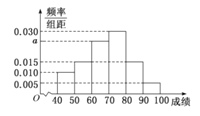
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中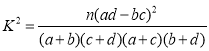 ,
,![]() .
.
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下扇形统计图:

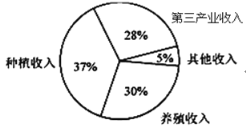
建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是( )
A.新农村建设后,种植收入略有增加.
B.新农村建设后,其他收入增加了一倍以上.
C.新农村建设后,养殖收入不变.
D.新农村建设后,种植收入在经济收入中所占比重大幅下降.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过椭圆的中心而平行于弦![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,设弦
,设弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在抛物线![]() 上,且点P的横坐标为2,以P为圆心,
上,且点P的横坐标为2,以P为圆心,![]() 为半径的圆(O为原点),与抛物线C的准线交于M,N两点,且
为半径的圆(O为原点),与抛物线C的准线交于M,N两点,且![]() .
.
(1)求抛物线C的方程;
(2)若抛物线的准线与y轴的交点为H.过抛物线焦点F的直线l与抛物线C交于A,B,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: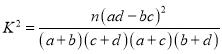
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型拟合的效果越好;
越小,说明模型拟合的效果越好;
③散点图中所有点都在回归直线附近;
④随机误差![]() 满足
满足![]() ,其方差
,其方差![]() 的大小可用来衡量预报精确度.
的大小可用来衡量预报精确度.
其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com