练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图所示的程序框图，则输出的k的值为（ ）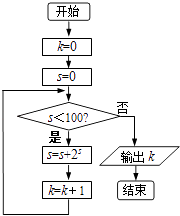

    A.7
    B.6
    C.5
    D.4

    【答案】D
    【解析】解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，
    可知：该程序的作用是：
    输出不满足条件S=0+1+2+8+…＜100时，k+1的值．
    第一次运行：满足条件，s=1，k=1；
    第二次运行：满足条件，s=3，k=2；
    第三次运行：满足条件，s=11＜100，k=3；满足判断框的条件，继续运行，
    第四次运行：s=1+2+8+211＞100，k=4，不满足判断框的条件，退出循环．
    故最后输出k的值为4．
    故选：D．
    分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是输出输出不满足条件S=0+1+2+8+…＜100时，k+1的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，锐角△ABC中， = ， = ，点M为BC的中点． （Ⅰ）试用 ， 表示 ；
    （Ⅱ）若| |=5，| |=3，sin∠BAC= ，求中线AM的长．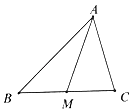

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|a≤x≤a+8}，B={x|x＜﹣1或x＞5}，
    （1）当a=0时，求A∩B，A∪（CRB）；
    （2）若A∪B=B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用m，n表示两条不同的直线，α，β表示两个不同的平面，给出下列命题： ①若m⊥n，m⊥α，则n∥α；
    ②若m∥α，α⊥β则m⊥β；
    ③若m⊥β，α⊥β，则m∥α；
    ④若m⊥n，m⊥α，n⊥β，则α⊥β，
    其中，正确命题是（ ）
    A.①②
    B.②③
    C.③④
    D.④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】请认真阅读下列程序框图，然后回答问题，其中n0∈N．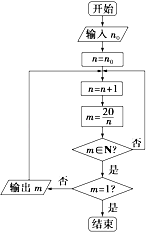
    （1）若输入n0=0，写出所输出的结果；
    （2）若输出的结果中有5，求输入的自然数n0的所有可能的值；
    （3）若输出的结果中，只有三个自然数，求输入的自然数n0的所有可能的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥 中，底面 是边长为 2 的正三角形，顶点 在底面上的射影为的中心，若为的中点，且直线与底面所成角的正切值为，则三棱锥外接球的表面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3+（1﹣a）x2﹣a（a+2）x+b（a，b∈R）．
    （1）若函数f（x）的图象过原点，且在原点处的切线斜率为﹣3，求a，b的值；
    （2）若曲线y=f（x）存在两条垂直于y轴的切线，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某景点拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为36米，其中大圆弧所在圆的半径为14米，设小圆弧所在圆的半径为米，圆心角为（弧度）.

    ⑴ 求关于的函数关系式；

    ⑵ 已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为16元/米，设花坛的面积与装饰总费用之比为，求关于的函数关系式，并求出的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，互相垂直的两条公路AP、AQ旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园AMN，要求点M在射线AP上，点N在射线AQ上，且直线MN过点C，其中AB=36米，AD=20米．记三角形花园AMN的面积为S． （Ⅰ）问：DN取何值时，S取得最小值，并求出最小值；
    （Ⅱ）若S不超过1764平方米，求DN长的取值范围．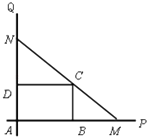

    查看答案和解析>>

    同步练习册答案