
| ||
| 2 |
| 1 |
| 2 |
| 5π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
| ||
| 6 |
| 5π |
| 6 |
| 5π |
| 3 |
| 5π |
| 3 |
| 1 |
| 2 |


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
| BM |
| MA |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省分校高三10月学习质量诊断理科数学试卷(解析版) 题型:解答题
(本题满分14分)
已知钝角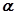 的顶点在原点,始边与
的顶点在原点,始边与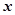 轴的正半轴重合,终边与单位圆相交于点
轴的正半轴重合,终边与单位圆相交于点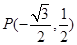 .
.
(Ⅰ) 求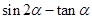 的值;
的值;
(Ⅱ) 若函数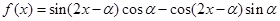 ,
试问该函数
,
试问该函数 的图象可由
的图象可由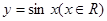 的图象经过怎样的平移和伸缩变换得到.
的图象经过怎样的平移和伸缩变换得到.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴一中分校高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
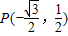 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴一中分校高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
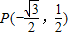 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com