
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点,以
边的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ..
..
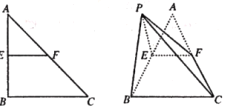
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 为线段
为线段![]() 上动点,求直线
上动点,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
【答案】(Ⅰ)见解析;
(Ⅱ)![]() .
.
【解析】
(Ⅰ)由题,易证得![]() ,即可证得结论;
,即可证得结论;
(Ⅱ)取BE的中点O,连接PO,易证得PO![]() ,然后以O为原点,建立直角坐标系,利用空间向量求得
,然后以O为原点,建立直角坐标系,利用空间向量求得![]() 与平面
与平面![]() 所成角的正弦值,求得其最大值即可.
所成角的正弦值,求得其最大值即可.
(Ⅰ)E,F分别为AB ,AC边的中点,所以![]()
因为![]()
![]()
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)取BE的中点O,连接PO,
由(1)知![]() 平面
平面![]() ,EF
,EF![]() 平面BCFE,,
平面BCFE,,
所以平面PBE![]() 平面BCFE
平面BCFE
因为PB=BE=PE,所以PO![]() ,
,
又因为PO![]() 平面PBE,平面PBE
平面PBE,平面PBE![]() 平面BCFE=BE
平面BCFE=BE
所以PO![]() .
.
过O作OM//BC交CF于M,分别以OB,OM,OP所在直线为
x,y,z轴建立空间直角坐标系,如图所示.

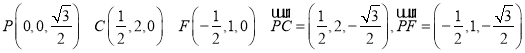
N为线段PF上一动点设![]() ,由,
,由,![]()
得
设平面PCF的法向量为![]()
则  即取
即取 ![]()
设直线BN与平面PCF所成角![]()


直线BN与平面PCF所成角的正弦值的最大值为![]()


科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
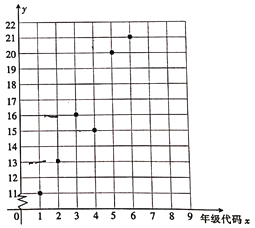
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数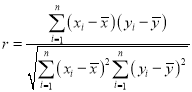 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=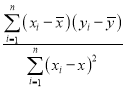 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 与
与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() ,
,![]() 两点.
两点.
(1)求线段![]() 中点
中点![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)若![]() 是(1)中点
是(1)中点![]() 的轨迹上的动点,求
的轨迹上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其中
,其中![]() ,点
,点![]() 是椭圆
是椭圆![]() 的右顶点,射线
的右顶点,射线![]() :
:![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设椭圆![]() 的长半轴、短半轴的长分别为
的长半轴、短半轴的长分别为![]() 、
、![]() ,当
,当![]() 的值在区间
的值在区间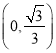 中变化时,求
中变化时,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,以![]() 为焦点,
为焦点,![]() 为顶点且开口方向向左的抛物线过点
为顶点且开口方向向左的抛物线过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司航拍宣传画报,为了凸显公司文化,选择如图所示的边长为2百米的正三角形![]() 空地进行布置拍摄场景,在
空地进行布置拍摄场景,在![]() 的中点
的中点![]() 处安装中央聚光灯,
处安装中央聚光灯,![]() 为边
为边![]() 上得可以自由滑动的动点,其中
上得可以自由滑动的动点,其中![]() 设置为普通色彩灯带(灯带长度可以自由伸缩),线段
设置为普通色彩灯带(灯带长度可以自由伸缩),线段![]() 部分需要材料
部分需要材料![]() (单位:百米)装饰用以增加拍摄效果因材料
(单位:百米)装饰用以增加拍摄效果因材料![]() 价格昂贵,所以公司要求采购
价格昂贵,所以公司要求采购![]() 材料使用不造成浪费.
材料使用不造成浪费.

(1)当![]() ,
,![]() 与
与![]() 垂直时,采购部需要采购多少百米材料
垂直时,采购部需要采购多少百米材料![]() ?
?
(2)为了增加拍摄动态效果需要,现要求点![]() 在
在![]() 边上滑动,且
边上滑动,且![]() ,则购买材料
,则购买材料![]() 的范围是多少才能满足动态效果需要又不会造成浪费.
的范围是多少才能满足动态效果需要又不会造成浪费.
查看答案和解析>>
科目:高中数学 来源: 题型:
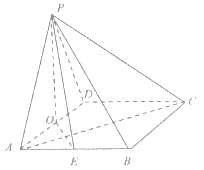
【题目】如图,四棱锥![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(I)证明:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 边上是否存在点
边上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,若存在,确定点
,若存在,确定点![]() 位置;若不存在,说明理由.
位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 中,
中,![]() 与
与![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形,![]() 为腰长为
为腰长为![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)试在平面![]() 内作一条直线,使直线上任意一点
内作一条直线,使直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明
平行,并给出详细证明
(2)求点![]() 到平面
到平面![]() 的距离
的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com