练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，AB=5，AC=12，BC=13，一只小蚂蚁从△ABC的内切圆的圆心处开始随机爬行，当蚂蚁（在三角形内部）与△ABC各边距离不低于1个单位时其行动是安全的，则这只小蚂蚁在△ABC内任意行动时安全的概率是（ ）
    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：由题意，与△ABC各边距离等于1个单位，组成的图形△A′B′C′与△ABC相似，内切圆半径为1， 设△ABC内切圆的半径为r，则 ，∴r=2，
    ∴△A′B′C′与△ABC的相似比为1：2，
    ∴△A′B′C′与△ABC的面积比为1：4，
    ∴这只小蚂蚁在△ABC内任意行动时安全的概率是 ，
    故选A
    由题意，与△ABC各边距离等于1个单位，组成的图形△A′B′C′与△ABC相似，内切圆半径为1，求出△A′B′C′与△ABC的面积比为1：4，即可求出这只小蚂蚁在△ABC内任意行动时安全的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知三棱锥中， ， ， 为中点， 为中点，且为正三角形．

    （1）求证： 平面；

    （2）若， ，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    (Ⅰ)若讨论的单调性；

    (Ⅱ)若过点可作函数图象的两条不同切线，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·江苏高考)如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.

    求证：(1)EF∥平面ABC；

    (2)AD⊥AC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某几何体的三视图如图所示，则该几何体的表面积为（ ）

    A.45
    B.
    C.
    D.60

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和Sn满足 ，且a1 ， a2+6，a3成等差数列．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn= ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班同学利用寒假进行社会实践活动，对岁的人群随机抽取人进行了一次生活习惯是

    否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得

    到如下统计表和各年龄段人数频率分布直方图：

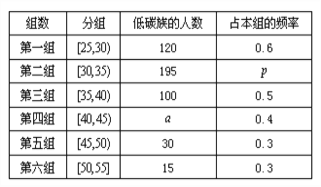
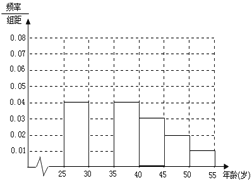
    （I）补全频率分布直方图并求、、的值；

    （II）从年龄段在的“低碳族”中采用分层抽样法抽取人参加户外低碳体验活动，其中选取人作为领队，求选取的名领队中恰有1人年龄在岁的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体ABCD-A1B1C1D中，S是B1D1的中点，E、F、G分别是BC、CD和SC的中点．求证：

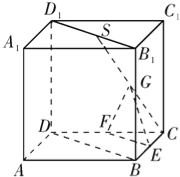
    （1）直线EG∥平面BDD1B1；

    （2）平面EFG∥平面BDD1B1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C的参数方程为： （φ为参数），直线l的极坐标方程为ρ（cosθ+sinθ）=4．
    （1）求曲线C的普通方程和直线l的直角坐标方程；
    （2）若点P在曲线C上，点Q在直线l上，求线段PQ的最小值．

    查看答案和解析>>

    同步练习册答案