
 ,
, 满足|
满足| |=2,|
|=2,| |=1,
|=1, ,
, 的夹角为60°,
的夹角为60°, =2x
=2x +7
+7 ,
, =
= +x
+x ,x∈R.
,x∈R. ,
, 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; •
• ,求f(x)在[-1,1]上的最大值与最小值.
,求f(x)在[-1,1]上的最大值与最小值.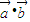 的值,再由
的值,再由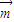 ,
,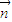 的夹角为钝角可知
的夹角为钝角可知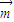 •
•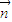 <0,代入即可解题.
<0,代入即可解题.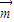 •
•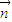 的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.
的值确定函数f(x)的解析式,再根据二次函数的单调性求出在[-1,1]上的最大值与最小值.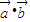 =|a||b|cos60°=2×1×cos60°=1,
=|a||b|cos60°=2×1×cos60°=1,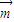 ,
,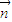 的夹角为钝角,得
的夹角为钝角,得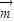 •
•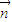 <0,且
<0,且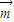 ≠λ
≠λ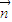
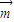 •
•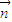 =(2x
=(2x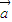 +7
+7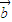 )•(
)•(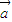 +x
+x )=2x
)=2x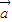 2+2
2+2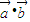 +2x2
+2x2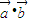 +7
+7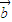 2
2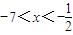 ,
, ≠λ
≠λ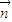
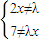 ,解得x≠
,解得x≠
 ;
;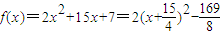 ,f(x)在[-1,1]上单调递增,
,f(x)在[-1,1]上单调递增,

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com