
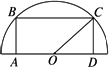
材料:为了美化环境,某房地产公司打算在所管辖的一个居民小区内的一块半圆形空地上,划出一个内接矩形辟为绿地,且使矩形的一边落在半圆的直径上,而另外两个顶点在半圆的圆周上,已知半圆的半径为30米.为了使绿地的面积最大,该公司请了本公司的一位设计师,设计出了这个半圆内接矩形的长与宽的关系.该设计师的计算过程如下:
如下图,设CD=x,则OD=![]() ,矩形的面积设为S,则
,矩形的面积设为S,则
S=2x·![]() =
=![]() .
.
所以当x2=450,即x=![]() 时,S有最大值,即此时矩形的面积最大.
时,S有最大值,即此时矩形的面积最大.
问题:现在我们已经学习了三角函数的有关知识,利用三角函数的知识该如何解决这一问题?
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com