
【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天时间与水深(单位:米)的关系表:
时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深 | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)请用一个函数来近似描述这个港口的水深y与时间t的函数关系;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上认为是安全的(船舶停靠时,船底只要不碰海底即可)。某船吃水深度(船底离地面的距离)为6.5米。
Ⅰ)如果该船是旅游船,1:00进港希望在同一天内安全出港,它至多能在港内停留多长时间(忽略进出港所需时间)?
Ⅱ)如果该船是货船,在2:00开始卸货,吃水深度以每小时0.5米的速度减少,由于台风等天气原因该船必须在10:00之前离开该港口,为了使卸下的货物尽可能多而且能安全驶离该港口,那么该船在什么整点时刻必须停止卸货(忽略出港所需时间)?
【答案】(1)![]() ;(2)Ⅰ)16小时,Ⅱ)见解析
;(2)Ⅰ)16小时,Ⅱ)见解析
【解析】分析:(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图.结合点的特征可认为函数解析式为![]() ;
;
(2)Ⅰ)由题意,![]() 就可以进出港,结合(1)的结论可得在同一天安全出港,在港内停留的最多时间是16小时.
就可以进出港,结合(1)的结论可得在同一天安全出港,在港内停留的最多时间是16小时.
Ⅱ)由题意结合三角函数的性质和一次函数的性质整理计算可得为了安全,货船最好在整点时刻6点之前停止卸货.
详解:
(1)以时间为横坐标,水深为纵坐标,在直角坐标系中画出散点图.如图.

根据图象,可考虑用函数![]() 刻画水深与时间之间的对应关系.
刻画水深与时间之间的对应关系.
从数据和图象![]() 可以得出
可以得出![]()
由![]() 得
得![]() ,
,
所以,这个港口水深与时间的关系可用![]() 近似描述.
近似描述.
(2)Ⅰ)由题意,![]() 就可以进出港,令
就可以进出港,令![]()
![]()
得![]() ,如图,
,如图,

在区间![]() 内,函数
内,函数![]() 与直线
与直线![]() 有两个交点,
有两个交点,
由![]() ,得
,得![]() ,由周期性得
,由周期性得![]() ,
,
由于该船从1:00进港,可以17:00离港,
所以在同一天安全出港,在港内停留的最多时间是16小时.
Ⅱ)设在时刻![]() 货船航行的安全水深为y,那么
货船航行的安全水深为y,那么![]() .
.
在同一坐标系下画出这两个函数的图象.

设![]() ,
,![]() 由
由![]()
且![]() 知,
知,
为了安全,货船最好在整点时刻6点之前停止卸货.


科目:高中数学 来源: 题型:
【题目】(本题满分12分.)
数列中{an},a1=8,a4=2,且满足an+2= 2an+1- an,
(1)求数列{an}的通项公式;
(2)设Sn=![]() ,求Sn
,求Sn
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间。
为了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各5台,在相同条件下进行测试,统计结果如下:
手机编号 | 1 | 2 | 3 | 4 | 5 |
A型待机时间(h) | 120 | 125 | 122 | 124 | 124 |
B型待机时间(h) | 118 | 123 | 127 | 120 | a |
已知A,B两个型号被测试手机待机时间的平均值相等。
(Ⅰ)求a的值;
(Ⅱ)求A型号被测试手机待机时间方差和标准差的大小;
(Ⅲ)从被测试的手机中随机抽取A,B型号手机各1台,求至少有1台的待机时间超过122小时的概率。
(注:n个数据![]() …
…![]() 的方差
的方差![]() …
…![]() ,其中
,其中![]() 为数据
为数据![]() …
…![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数组成的等比数列{an}的前项和为Sn , 且满足8a4=a7 , S7=254.
(1)求数列{an}的通项公式;
(2)对n∈N* , bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,面![]() 为正方形,面
为正方形,面![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
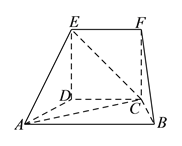
(I)求证: ![]() 平面
平面![]() .
.
(II)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足![]() ,其中a≠0,q:实数x满足
,其中a≠0,q:实数x满足![]() .
.
(I)若a=1,且p∧q为真,求实数x的取值范围.
(II)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
(![]() )若
)若![]() 关于的方程
关于的方程![]() 有区间
有区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(相等的实数根算一个).
的取值范围(相等的实数根算一个).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com