
【题目】如图,梯形![]() 与矩形
与矩形![]() 所在平面相互垂直,
所在平面相互垂直, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的侧面积.
的侧面积.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线l过点P(3,4)
(1)它在y轴上的截距是在x轴上截距的2倍,求直线l的方程.
(2)若直线l与![]() 轴,
轴,![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
参考公式及数据: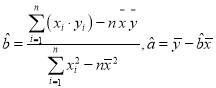
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)若函数f(x)的图像中相邻两条对称轴间的距离不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若函数f(x)的最小正周期为π,且当x∈![]() 时,f(x)的最大值是
时,f(x)的最大值是![]() ,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
,求函数f(x)的最小值,并说明如何由函数y=sin2x的图象变换得到函数y=f(x)的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
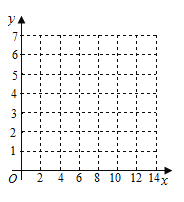
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() ,
, ![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求△
,求△![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得![]() ,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?

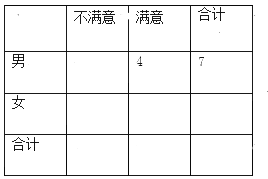
附:

(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点在
的两焦点在![]() 轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为
轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com