

分析 (1)通过观察特殊行得出规律,可判断此表第n行数的规律.
(2)运用等差数列的求和公式求解.
(3)先运用公式判断是第几行的数,再判断是第几个数.
解答 解:(1)通过观察前几行得出规律可判断:第n+1行的第一个数是2n,
∴第n行的最后一个数是2n-1.
(2)2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1)
=$\frac{{2}^{n-1}+{2}^{n}-1}{2}$,所求此表第n行的各个数之和是$\frac{{2}^{n-1}+{2}^{n}-1}{2}$.
(3)∵210=1 024,211=2 048,1 024<2 010<2 048,
∴2 010在第11行,该行第1个数是210=1 024.
由2 015-1 024+1=992,知2 015是第11行的第992个数.
点评 本题考查了等差数列的概念,公式性质在数阵中的应用,加强了数列的运用能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
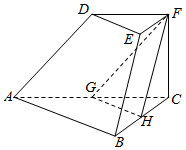 如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 6 | 7 | 9 | 10 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com