
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是
是![]() 轴上关于原点
轴上关于原点![]() 对称的两定点,点
对称的两定点,点![]() 满足
满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线分别与
的中垂线分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,问
,问![]() 是否成立?若成立,求出直线
是否成立?若成立,求出直线![]() 的方程;若不成立,请说明理由.
的方程;若不成立,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 不成立,理由详见解析.
不成立,理由详见解析.
【解析】
(1)根据椭圆的定义,可以判断出点![]() 的轨迹是焦点为
的轨迹是焦点为![]() 、
、![]() ,长轴长为4的椭圆,确定出
,长轴长为4的椭圆,确定出![]() ,进而求得
,进而求得![]() ,得到椭圆的方程;
,得到椭圆的方程;
(2)该题可以从三个角度去分析,一是设直线方程为![]() ,根据题意列出等式,无解,从而确定不成立;二是设直线方程为
,根据题意列出等式,无解,从而确定不成立;二是设直线方程为![]() ,根据三角形全等去分析,推出矛盾,不成立,三是利用点差法确定出直线的斜率,写出点斜式方程,列式,推出矛盾,从而不成立,得到结果.
,根据三角形全等去分析,推出矛盾,不成立,三是利用点差法确定出直线的斜率,写出点斜式方程,列式,推出矛盾,从而不成立,得到结果.
(1)因为![]() ,
,
所以点![]() 的轨迹是焦点为
的轨迹是焦点为![]() 、
、![]() ,长轴长为4的椭圆,
,长轴长为4的椭圆,
设椭圆方程为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)解法一:
直线![]() 的斜率必存在且不为0,设
的斜率必存在且不为0,设![]() 方程为
方程为![]() ,
,
由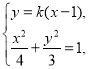 消去
消去![]() 整理得
整理得
![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,
故点![]() 的横坐标为
的横坐标为![]() ,所以
,所以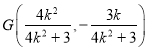 ,
,
设![]() ,因为
,因为![]() ,所以
,所以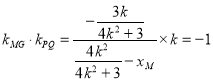 ,
,
解得![]() ,所以
,所以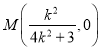 ,
,
要使![]() ,只需
,只需![]() ,
,
即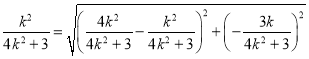 ,
,
整理得![]() ,因为
,因为![]() ,所以此方程无实根,
,所以此方程无实根,
所以![]() 不成立.
不成立.
解法二:
直线![]() 的斜率必存在且不为0,设
的斜率必存在且不为0,设![]() 方程为
方程为![]() ,
,
由 消去
消去![]() 整理得
整理得![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
故点![]() 的纵坐标为
的纵坐标为![]() ,
,
所以![]() ,
,
因为直线![]() 的斜率为
的斜率为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
令![]() ,则
,则![]() ,
,
所以点![]() 的纵坐标为
的纵坐标为![]() ,即
,即![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
要使得![]() ,则必须
,则必须![]() ,
,
因为上式不成立,所以![]() 不成立.
不成立.
解法三:
设![]() ,因为
,因为![]() 在曲线
在曲线![]() 上,且
上,且![]()
所以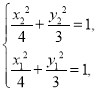 两式相减并整理得
两式相减并整理得![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,所以点
,所以点![]() 的纵坐标
的纵坐标![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
要使得![]() ,则必须
,则必须![]() ,
,
因为上式不成立,所以![]() 不成立.
不成立.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】从①前![]() 项和
项和![]() ,②
,②![]() ,③
,③![]() 且
且![]() ,这三个条件中任选一个,补充到下面的问题中,并完成解答.
,这三个条件中任选一个,补充到下面的问题中,并完成解答.
在数列![]() 中,
中,![]() ,_______,其中
,_______,其中![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() 成等比数列,其中
成等比数列,其中![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地中小学生的近视形成原因,教育部门委托医疗机构对该地所有中小学生的视力做了一次普查.现该地中小学生人数和普查得到的近视情况分别如图1和图2所示.
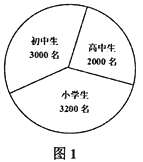
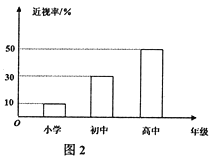
(1)求该地中小学生的平均近视率(保留两位有效数字);
(2)为调查中学生用眼卫生习惯,该地用分层抽样的方法从所有初中生和高中生中确定5人进行问卷调查,再从这5人中随机选取2人继续访谈,则此2人全部来自高中年级的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() 和
和![]() ,过
,过![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线交直线
轴垂直的直线交直线![]() 于点
于点![]() .设
.设![]() ,已知当
,已知当![]() 时,
时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:无论![]() 如何变化,直线
如何变化,直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: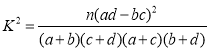 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有3个不同值班地点,每个值班地点需配一名医务人员和两名警察,现将3名医务人员(1男2女)和6名警察(4男2女)分配到这3个地点去值班,要求每个值班地点至少有一名女性,则共有______种不同分配方案.(用具体数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为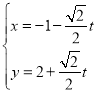 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com