
分析 x、y∈(-2,2)且xy=1,可得y=$\frac{1}{x}$(x≠0).化简变形$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$=1+$\frac{7}{9-(4{x}^{2}+\frac{2}{{x}^{2}})}$,利用基本不等式的性质即可得出.
解答 解:∵x、y∈(-2,2)且xy=1,∴y=$\frac{1}{x}$(x≠0).
则$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$=$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-\frac{1}{{x}^{2}}}$=$\frac{2}{2-{x}^{2}}$+$\frac{1}{4{x}^{2}-1}$+1=1+$\frac{7}{9-(4{x}^{2}+\frac{2}{{x}^{2}})}$≥1+$\frac{7}{9-2×2\sqrt{2{x}^{2}•\frac{1}{{x}^{2}}}}$=$\frac{16+4\sqrt{2}}{7}$,当且仅当x2=$\frac{\sqrt{2}}{2}$,y2=$\sqrt{2}$时取等号.
∴$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$的最小值为$\frac{16+4\sqrt{2}}{7}$,
故答案为:$\frac{16+4\sqrt{2}}{7}$.
点评 本题考查了基本不等式的性质,考查了变形能力、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
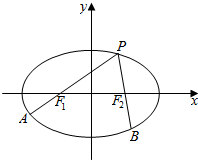 如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )
如图,F1F2为椭圆C:$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的左、右焦点,点P为椭圆C上一点,延长PF1、,PF2分别交椭圆C于A,B.若$\overrightarrow{P{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,$\overrightarrow{P{F}_{2}}$=$λ\overrightarrow{{F}_{2}B}$,则λ=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com