
【题目】如图,点![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 上,
上, ![]() 垂直于圆
垂直于圆![]() 所在的平面,
所在的平面, ![]() 为
为![]() 的重心.
的重心.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|
(1)若函数y=f(x)+x在R上是增函数,求实数a的取值范围;
(2)若对任意x∈[1,2]时,函数f(x)的图像恒在y=1图像的下方,求实数a的取值范围;
(3)设a≥2时,求f(x)在区间[2,4]内的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M. 
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连结AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001,002,003,…,800进行编号.
(Ⅰ)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号:(下面摘取了第7行至第9行)

(Ⅱ)抽的100人的数学与地理的水平测试成绩如下表:

成绩优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求![]() 的值.
的值.
(Ⅲ)将![]() ,
, ![]() 的
的![]() 表示成有序数对
表示成有序数对![]() ,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对
,求“地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,求出最大的整数
的图象的下方?若存在,求出最大的整数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的以往各年的宣传费用支出![]() (万元)与销售量
(万元)与销售量![]() (万件)之间有如下对应数据
(万件)之间有如下对应数据
| 2 | 4 | 5 | 6 | 8 |
| 4 | 3 | 6 | 7 | 8 |
(1)试求回归直线方程;
(2)设该产品的单件售价与单件生产成本的差为![]() (元),若
(元),若![]() 与销售量
与销售量![]() (万件)的函数关系是
(万件)的函数关系是![]() ,试估计宣传费用支出
,试估计宣传费用支出![]() 为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
为多少万元时,销售该产品的利润最大?(注:销售利润=销售额-生产成本-宣传费用)
(参考数据与公式: ![]() ,
, ![]() ,
, 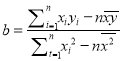 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com