�����У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ƿ֣�����ʱ�����ڴ���ϰ���ѡ��Ŀ��Ӧ��������������У�
��1��ѡ��4-2��������任
��֪������

������ֵ��=-1����Ӧ��һ����������

��
���������M��
����������C�ھ���M�������µõ��ķ���Ϊx
2+2y
2=1��������C�ķ��̣�
��2��ѡ��4-4������ϵ���������
��ֱ������ϵxOy�У�����C�IJ�������Ϊ

Ϊ������������P���Ը�ֱ������ϵ��ԭ��O��Ϊ���㣬x���������Ϊ����ļ�����ϵ�µķ���Ϊp
2-4pcos��+3=0��
����������C����ͨ���̺�����P��ֱ�����귽�̣�
����������C������P�Ľ���ΪA��B����|AB|��
��3��ѡ��4-5������ʽѡ��
��֪����f��x��=|x+1|+|x-2|������ʽt��f��x����x��R�Ϻ������
������ʵ��t��ȡֵ��Χ��
����t�����ֵΪT������ʵ��a��b��c����a
2+b
2+c
2=T����a+2b+c�����ֵ��

 ������ֵ��=-1����Ӧ��һ����������
������ֵ��=-1����Ӧ��һ���������� ��
�� Ϊ������������P���Ը�ֱ������ϵ��ԭ��O��Ϊ���㣬x���������Ϊ����ļ�����ϵ�µķ���Ϊp2-4pcos��+3=0��
Ϊ������������P���Ը�ֱ������ϵ��ԭ��O��Ϊ���㣬x���������Ϊ����ļ�����ϵ�µķ���Ϊp2-4pcos��+3=0��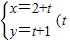 Ϊ����������ȥ����t������ͨ���̣��ٸ��ݼ������ֱ�����귽�̵Ļ�����ʽ�������C�ڼ�����ϵ�еķ��̣�
Ϊ����������ȥ����t������ͨ���̣��ٸ��ݼ������ֱ�����귽�̵Ļ�����ʽ�������C�ڼ�����ϵ�еķ��̣�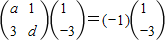 ����
����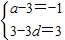 ������2�֣�
������2�֣�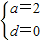 ������
������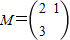 ������3�֣�
������3�֣�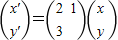 ����
����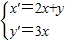 ������5�֣�
������5�֣�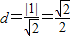 ������
������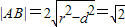 ������7�֣�
������7�֣�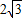 ������6�֣�
������6�֣�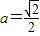 ��
��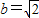 ��
��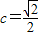 ʱ�Ⱥų���������7�֣�
ʱ�Ⱥų���������7�֣�

