【题目】已知双曲线中心在原点且一个焦点为 
，直线 
与其相交于 
， 
两点， 
中点的横坐标为 
，则此双曲线的方程是（ ）
A.
B.
C.
D.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体，截面为ABC，已知A1B1＝B1C1＝2，∠A1B1C1＝90°，AA1＝4，BB1＝3，CC1＝2，求：
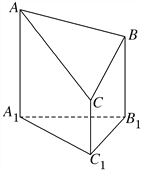
(Ⅰ)该几何体的体积；
(Ⅱ)截面ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某教育集团为了办好人民满意的教育，每年底都随机邀请
名学生家长代表对集团内甲、乙两所学校进行人民满意的民主测评（满意度最高分
，最低分
，分数越高说明人民满意度越高，分数越低说明人民满意度越低）.去年测评的数据如下：
甲校：
；
乙校：
.
（1）分别计算甲、乙两所学校去年人民满意度测评数据的平均数、中位数；
（2）分别计算甲、乙两所学校去年人民满意度的方差；
（3）根据以上数据你认为这两所学校哪所学校人民满意度比较好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知x＞0，由不等式x+ 
≥2 
=2，x+ 
= 
≥3 
=3，…，可以推出结论：x+ 
≥n+1（n∈N*），则a=（ ）
A.2n
B.3n
C.n2
D.nn
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】记数列
的前
项和为
，若存在实数
，使得对任意的
，都有
，则称数列为“和有界数列”. 下列命题正确的是( )
A. 若是等差数列，且首项
，则是“和有界数列”
B. 若是等差数列，且公差
，则是“和有界数列”
C. 若是等比数列，且公比
，则是“和有界数列”
D. 若是等比数列，且是“和有界数列”，则的公比
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对30名六年级学生进行了问卷调查，得到如下列联表（平均每天喝500ml以上为常喝，体重超过50kg为肥胖）：
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人，抽到肥胖的学生的概率为 
．
（1）请将上面的列联表补充完整；
（2）是否有99.5%的把握认为肥胖与常喝碳酸饮料有关？说明你的理由；
（3）现从常喝碳酸饮料且肥胖的学生中（2名女生），抽取2人参加电视节目，则正好抽到一男一女的概率是多少
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2= 
，其中n=a+b+c+d）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
