
分析 (1)利用配方法求解即可.
(2)利用换底公式以及对数运算法则求解即可.
解答 解:$(1)∵{x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}}=3$∴${({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})}^{2}=x+2+{x}^{-1}=9$,∴x+x-1=7.
(2)∵$lo{g}_{5}12=\frac{lg12}{lg5}$,且lg2+lg3=lg(2×3)=lg6=a+b,
∴lg12=lg(6×2)=lg6+lg2=2a+b,
$lg5=lg\frac{10}{2}=lg10-lg2=1-a$,
∴$lo{g}_{5}12=\frac{lg12}{lg5}=\frac{2a+b}{1-a}$
点评 本题考查有理指数幂以及对数运算法则的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,α⊥β,则l∥β | B. | 若l∥α,α∥β,则l∥β或l⊆β | ||
| C. | 若l⊥α,α∥β,则l⊥β | D. | 若l⊥α,α⊥β,则l∥β或l⊆β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
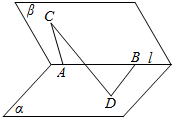 如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.
如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若二面角α-l-β的大小为$\frac{π}{3}$,AB=AC=2,CD=$\sqrt{11}$,则BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $±\frac{{\sqrt{2}}}{3}$ | C. | $±\frac{{\sqrt{2}}}{4}$ | D. | $±\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com