
【题目】如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.
(I)求证:A′D⊥面A′EF;
(Ⅱ)试探究:在图1中,F在什么位置时,能使折起后的几何体中EF∥平面AMN,并给出证明.
【答案】证明:(Ⅰ)∵A′D⊥A′E,A′D⊥A′F,
又A′E∩A′F=A′,A′E面A′EF,A′F面A′EF,
∴A′D⊥面A′EF.
(Ⅱ)当点F为BC的中点时,EF∥面A′MN.
证明如下:当点F为BC的中点时,
在图(1)中,E,F分别是AB,BC的中点,
所以EF∥AC,
即在图(2)中有EF∥MN.
又EF面A′MN,MN面A′MN,
所以EF∥面A′MN.
【解析】(Ⅰ)由题意可得,A′D⊥A′E,A′D⊥A′F,A′E∩A′F=A′,利用线面垂直的判定定理即可证得结论;
(Ⅱ)当点F为BC的中点时,EF∥面A′MN.在图(1)中,E,F分别是AB,BC的中点,可得EF∥AC,而M∈AC,N∈AC,从而可得EF∥MN,继而有EF∥平面AMN.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】给出下列命题:①定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,则
,则![]() 一定不是
一定不是![]() 上的减函数;
上的减函数;
②用反证法证明命题“若实数![]() ,满足
,满足![]() ,则
,则![]() 都为0”时,“假设命题的结论不成立”的叙述是“假设
都为0”时,“假设命题的结论不成立”的叙述是“假设![]() 都不为0”;
都不为0”;
③把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得到的图象的函数解析式为
个单位长度,所得到的图象的函数解析式为![]() ;
;
④“![]() ”是“函数
”是“函数![]() 为奇函数”的充分不必要条件.
为奇函数”的充分不必要条件.
其中所有正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: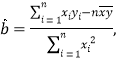
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 过点
过点![]() ,求直线
,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线交于
与曲线交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了及时向群众宣传“十九大”党和国家“乡村振兴”战略,需要寻找一个宣讲站,让群众能在最短的时间内到宣讲站.设有三个乡镇,分别位于一个矩形![]() 的两个顶点
的两个顶点![]() 及
及![]() 的中点
的中点![]() 处,
处,![]() ,
,![]() ,现要在该矩形的区域内(含边界),且与
,现要在该矩形的区域内(含边界),且与![]() 等距离的一点
等距离的一点![]() 处设一个宣讲站,记
处设一个宣讲站,记![]() 点到三个乡镇的距离之和为
点到三个乡镇的距离之和为![]() .
.
(Ⅰ)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试利用(Ⅰ)的函数关系式确定宣讲站![]() 的位置,使宣讲站
的位置,使宣讲站![]() 到三个乡镇的距离之和
到三个乡镇的距离之和![]() 最小.
最小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若对所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,则m的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com