
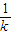 次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为
次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为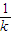 +1次,然后分别求出相应的概率,利用数学期望公式解之即可;
+1次,然后分别求出相应的概率,利用数学期望公式解之即可;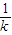 次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为
次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为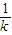 +1次.
+1次.| ξ | 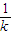 | 1+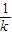 |
| P | 0.9k | 1-0.9k |
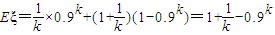 .(5分)
.(5分)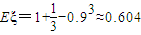 ;
;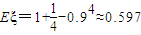 ;
;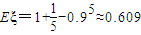 .(9分)
.(9分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)每个人的血分别化验,这需要n次;
(2)按k个人一组进行分组,把k个人的血混在一起化验,如果结果是阴性的,那么这k个人只作一次化验就够了,如果结果是阳性的,那么就必须对这k个人逐一化验,即对这k个人进行k+1次化验,假定对所有人来说,化验是阳性反应的概率都是p,且这些人的化验是相互独立的,求按第二种方案这n个人平均需要化验的次数.
查看答案和解析>>
科目:高中数学 来源:武汉模拟 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com