
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围;
内有两个极值点,求实数a的取值范围;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的![]() ,
,![]() .
.
【答案】(1)递减区间为![]() ,递增区间为
,递增区间为![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)求解![]() ,利用
,利用![]() ,
,![]() ,解不等式求解单调递增区间,单调递减区间;
,解不等式求解单调递增区间,单调递减区间;
(2)![]() ,其中
,其中![]() ,再次构造函数令
,再次构造函数令![]() ,分析
,分析![]() 的零点情况,
的零点情况,![]() ,令
,令![]() ,
,![]() ,列表分析得出
,列表分析得出![]() 单调性,判断
单调性,判断![]() ,分类讨论求解①若
,分类讨论求解①若![]() ,②若
,②若![]() ,③若
,③若![]() ,
,![]() 的单调性,
的单调性,![]() 最大值,最小值,确定有无零点转化为极值即可;
最大值,最小值,确定有无零点转化为极值即可;
(3)存在![]() :
:![]() ,
,![]() 恒成立,再运用导数判断证明,令
恒成立,再运用导数判断证明,令![]() ,
,![]() ,
,![]() ,求解最大值,得出
,求解最大值,得出![]() 即可.
即可.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,
,![]() ,列表分析
,列表分析
x |
| 1 |
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)![]() ,
,![]() ,其中
,其中![]() ,
,
令![]() ,分析
,分析![]() 的零点情况.
的零点情况.
![]() ,令
,令![]() ,
,![]() ,列表分析
,列表分析
x |
|
|
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
![]() ,
,
而![]() ,
,![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,
,
故![]() 在
在![]() 内没有极值点,舍;
内没有极值点,舍;
②若![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
因此![]() 在
在![]() 有两个零点,设为
有两个零点,设为![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() 单调递增,此时
单调递增,此时![]() 在
在![]() 内有两个极值点;
内有两个极值点;
③若![]() ,则
,则![]() ,
,![]() ,
,
![]() ,因此
,因此![]() 在
在![]() 有一个零点,
有一个零点,
![]() 在
在![]() 内有一个极值点;
内有一个极值点;
综上所述,实数a的取值范围为![]() .
.
(3)存在![]() :
:![]() ,
,![]() 恒成立.
恒成立.
证明如下:
由(2)得![]() 在
在![]() 上单调递增,
上单调递增,
且![]() ,
,![]() .
.
因为当![]() 时,
时,![]() (*),所以
(*),所以![]() .
.
故![]() 在
在![]() 上存在唯一的零点,设为
上存在唯一的零点,设为![]() .
.
由
x |
|
|
|
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
知![]() ,
,![]() .
.
又![]() ,而
,而![]() 时,
时,![]() (**),
(**),
所以![]() .
.
即![]() ,
,![]() .
.
所以对任意的正数a,都存在实数![]() ,使对任意的
,使对任意的![]() ,使
,使![]() .
.
补充证明(*):
令![]() ,
,![]() .
.![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 时,
时,![]() ,即
,即![]() .
.
补充证明(**)
令![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() 时,
时,![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
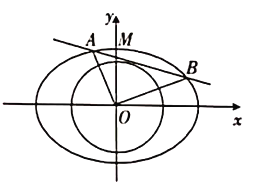
(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 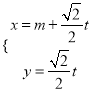 (
(![]() 是参数).
是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M为
,M为![]() 的中点.
的中点.
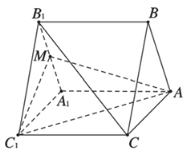
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿侧棱
,且沿侧棱![]() 展开三棱柱的侧面,得到的侧面展开图的对角线长为
展开三棱柱的侧面,得到的侧面展开图的对角线长为![]() ,求作点
,求作点![]() 在平面
在平面![]() 内的射影H,请说明作法和理由,并求线段AH的长.
内的射影H,请说明作法和理由,并求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生的数学与语文的水平测试成绩抽样统计如下表:
数学(x)
语文(y) | 90分~100分 (数A) | 80分~90分 (数B) | 60分~80分 (数C) |
90分~100分 (语A) | 20 | 7 | 5 |
80分~90分 (语B) | 18 | 9 | 6 |
60分~80分 (语C) | 4 | a | b |
设x,y分别表示数学成绩与语文成绩,若抽取学生n人,成绩在90分~100分者记为A等级(优秀),成绩在80分~90分者记为B等级(良好),成绩在60分~80分者记为C等级(及格).例如:表中数学成绩为A等级的共有![]() 人.已知x与y均为B等级的概率是0.09.
人.已知x与y均为B等级的概率是0.09.
(1)若在该样本中,数学成绩良好率是30%,求a,b的值;
(2)在语文成绩为C等级的学生中,已知![]() ,
,![]() ,求数学成绩为B等级的人数比C等级的人数少的概率.
,求数学成绩为B等级的人数比C等级的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com