
【题目】在直角坐标系xOy上取两个定点A1(![]() ,0),A2(
,0),A2(![]() ,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
(1)求直线A1N1与A2N2交点M的轨迹C的方程;
(2)过R(3,0)的直线与轨迹C交于P,Q,过P作PN⊥x轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() (λ>1),求证:
(λ>1),求证:![]() .
.
【答案】(1)![]() 1(x≠±
1(x≠±![]() );(2)证明见解析
);(2)证明见解析
【解析】
(1)根据题意先写出两直线的方程,再根据条件化简即可求得答案;
(2)设P(x1,y1),Q(x2,y2),设l:x=ty+3,联立直线与椭圆的方程,由韦达定理得y1+y2![]() 且y1y2
且y1y2![]() ,根据题意得 x1﹣3=λ(x2﹣3),y1=λy2,再代入即可证明结论.
,根据题意得 x1﹣3=λ(x2﹣3),y1=λy2,再代入即可证明结论.
(1)解:依题意知直线A1N1的方程为:y![]() (x
(x![]() )…①;
)…①;
直线A2N2的方程为:y![]() (x
(x![]() )…②
)…②
设Q(x,y)是直线A1N1与A2N2交点,①、②相乘,得y2![]() (x2﹣6)
(x2﹣6)
由mn=2整理得:![]() 1
1
∵N1、N2不与原点重合,可得点A1,A2不在轨迹M上,
∴轨迹C的方程为![]() 1(x≠±
1(x≠±![]() );
);
(2)证明:设l:x=ty+3,代入椭圆方程消去x,得(3+t2)y2+6ty+3=0.
设P(x1,y1),Q(x2,y2),N(x1,﹣y1),可得y1+y2![]() 且y1y2
且y1y2![]() ,
,
![]() ,可得(x1﹣3,y1)=λ(x2﹣3,y2),∴x1﹣3=λ(x2﹣3),y1=λy2,
,可得(x1﹣3,y1)=λ(x2﹣3,y2),∴x1﹣3=λ(x2﹣3),y1=λy2,
证明![]() ,只要证明(2﹣x1,y1)=λ(x2﹣2,y2),∴2﹣x1=λ(x2﹣2),
,只要证明(2﹣x1,y1)=λ(x2﹣2,y2),∴2﹣x1=λ(x2﹣2),
只要证明![]() ,只要证明2t2y1y2+t(y1+y2)=0,
,只要证明2t2y1y2+t(y1+y2)=0,
由y1+y2![]() 且y1y2
且y1y2![]() ,代入可得2t2y1y2+t(y1+y2)=0,
,代入可得2t2y1y2+t(y1+y2)=0,
∴![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() ,且该椭圆的短轴端点与两焦点
,且该椭圆的短轴端点与两焦点![]() ,
,![]() 的张角为直角.
的张角为直角.
(1)求椭圆E的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与椭圆E相交于点P,Q,直线AP,AQ与y轴相交于M,N两点,求
与椭圆E相交于点P,Q,直线AP,AQ与y轴相交于M,N两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
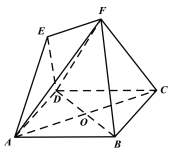
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 为曲线
为曲线![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是有如下性质:如果常数
是有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)如果函数![]() 的值域为
的值域为![]() ,求b的值;
,求b的值;
(2)研究函数![]() (常数
(常数![]() )在定义域内的单调性,并说明理由;
)在定义域内的单调性,并说明理由;
(3)对函数![]() 和
和![]() (常数
(常数![]() )作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数![]() (n是正整数)在区间
(n是正整数)在区间![]() 上的最大值和最小值.(可利用你的研究结论)
上的最大值和最小值.(可利用你的研究结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
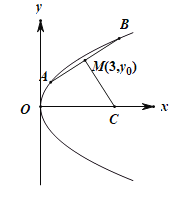
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com