
【题目】现有流量均为![]() 的两条河流
的两条河流![]() 汇合于某处后,不断混合,它们的含沙量分别为
汇合于某处后,不断混合,它们的含沙量分别为![]() 和
和![]() .假设从汇合处开始,沿岸设有若干个观测点,两股水流在流往相邻两个观测点的过程中,其混合效果相当于两股水流在1秒内交换
.假设从汇合处开始,沿岸设有若干个观测点,两股水流在流往相邻两个观测点的过程中,其混合效果相当于两股水流在1秒内交换![]() 的水量,其交换过程为从A股流入B股
的水量,其交换过程为从A股流入B股![]() 的水量,经混合后,又从B股流入A股
的水量,经混合后,又从B股流入A股![]() 水并混合,问从第几个观测点开始,两股河水的含沙量之差小于
水并混合,问从第几个观测点开始,两股河水的含沙量之差小于![]() .(不考虑泥沙沉淀).
.(不考虑泥沙沉淀).
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:高中数学 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
B.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
C.若随机变量![]() 服从二项分布:
服从二项分布:![]() ,则
,则![]() ;
;
D.![]() 是
是![]() 的充分不必要条件.
的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,对于一切
时,对于一切![]() ,函数
,函数![]() 在区间
在区间![]() 内总存在唯一零点,求
内总存在唯一零点,求![]() 的取值范围;
的取值范围;
(2)若![]() 区间
区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的零点为
内的零点为![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() ,…的增减性,并说明理由.
,…的增减性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个半径为1千米的扇形景点的平面示意图,![]() .原有观光道路OC,且
.原有观光道路OC,且![]() .为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且
.为便于游客观赏,景点管理部门决定新建两条道路PQ、PA,其中P在原道路OC(不含端点O、C)上,Q在景点边界OB上,且![]() ,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是
,同时维修原道路的OP段,因地形原因,新建PQ段、PA段的每千米费用分别是![]() 万元、
万元、![]() 万元,维修OP段的每千米费用是
万元,维修OP段的每千米费用是![]() 万元.
万元.
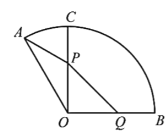
(1)设![]() ,求所需总费用
,求所需总费用![]() ,并给出
,并给出![]() 的取值范围;
的取值范围;
(2)当P距离O处多远时,总费用最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com