
【题目】已知函数f(x)=x3-2x2+x+a,g(x)=-2x+![]() ,若对任意的x1∈[-1,2],存在x2∈[2,4],使得f(x1)=g(x2),则实数a的取值范围是________.
,若对任意的x1∈[-1,2],存在x2∈[2,4],使得f(x1)=g(x2),则实数a的取值范围是________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为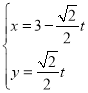 ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车,购车费用是10万元,第一年维修费用是0.2万元,以后逐年递增0.2万元,且每年的保险费、养路费、汽油费等约为0.9万元.
(1)设这种汽车使用![]() 年(
年(![]() )的维修费用的和为
)的维修费用的和为![]() 万元,求
万元,求![]() 的表达式;
的表达式;
(2)这种汽车使用多少年时,它的年平均费用最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知f(x)=|x+a|(a∈R).
(1)若f(x)≥|2x﹣1|的解集为[0,2],求a的值;
(2)若对任意x∈R,不等式f(x)+|x﹣a|≥3a﹣2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的![]() ,男生喜欢抖音的人数占男生人数的
,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() 若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取了100名学生的笔试成绩,按成绩分组,得到的频率分布如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.00 | |
(1)请求出频率分布表中①、②处应填的数据;
(2)为了能选拔最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样法抽取6名学生进入第二轮面试,问第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行的面试,求第4组有一名学生被考官A面试的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com