分析:(1)连接BE,可根据射影相等的两条斜线段相等证得BD=DC,再根据相等的斜线段的射影相等得到AB=AC;
(2)求B1C与平面BCD所成的线面角,只需求点B1到面BDC的距离即可,作AG⊥BD于G,连GC,∠AGC为二面角A-BD-C的平面角,在三角形AGC中求出GC即可.
解答:
解:如图
(I)连接BE,∵ABC-A
1B
1C
1为直三棱柱,
∴∠B
1BC=90°,
∵E为B
1C的中点,∴BE=EC.
又DE⊥平面BCC
1,
∴BD=DC(射影相等的两条斜线段相等)而DA⊥平面ABC,
∴AB=AC(相等的斜线段的射影相等).
(II)求B
1C与平面BCD所成的线面角,
只需求点B
1到面BDC的距离即可.
作AG⊥BD于G,连GC,则GC⊥BD,
∠AGC为二面角A-BD-C的平面角,∠AGC=60°
不妨设
AC=2,则AG=2,GC=4
在RT△ABD中,由AD•AB=BD•AG,易得
AD=设点B
1到面BDC的距离为h,B
1C与平面BCD所成的角为α.
利用
S△B1BC•DE=S△BCD•h,
可求得h=
2,又可求得
B1C=4sinα==,∴α=30°.
即B
1C与平面BCD所成的角为30°.
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

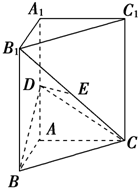 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1. 解:如图
解:如图

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案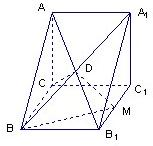 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=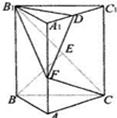 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.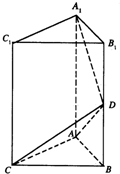 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.