
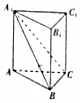
 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 证明AD⊥平面A1BC,得出∠ACD即为直线AC与平面A1BC所成的角,求出AC=$\sqrt{2}$,AD=$\frac{\sqrt{2}}{2}$,即可得出结论.
解答  解:如图,AB1∩A1B=D,连结CD,
解:如图,AB1∩A1B=D,连结CD,
∵AA1=AB,∴AD⊥A1B,
∵平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
∴AD⊥平面A1BC,
则CD是AC在平面A1BC内的射影,
∴∠ACD即为直线AC与平面A1BC所成的角,
又BC?平面A1BC,
所以AD⊥BC,
因为三棱柱ABC---A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB?侧面A1ABB1,故AB⊥BC
∵AA1=AB=BC=2,∴AC=$\sqrt{2}$,AD=$\frac{\sqrt{2}}{2}$
∴sin∠ACD=$\frac{1}{2}$,∴∠ACD=$\frac{π}{6}$,
故选A.
点评 本题考查直线与平面垂直的判定定理的应用,直线与平面所成角的求法,考查计算能力以及逻辑推理能力.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
| A. | 0.56 | B. | 0.44 | C. | 0.26 | D. | 0.14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com